Snap rounding
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
Содержание
Введение
Snap rounding (фиксирование выравнивания) — это алгоритм, который восстанавливает топологию множества отрезков, координаты которого заданны с некоторой погрешностью.
Мотивация
Пусть у нас есть множество отрезков, чьи координаты были получены с некоторой абсолютной погрешностью. В такой структуре может быть нарушена топология, а это может повлиять на работу других алгоритмов над этой структурой.
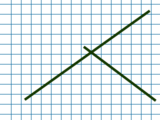
Например, если у нас появилось ложное пересечение (рисунок 1) мы можем получить отрицательное "расстояние" до прямой, если ожидаем, что все точки лежат с одной стороны относительное неё. Ещё, из-за недостаточной точности, может быть нарушена замкнутость контура (рисунок 2), что приведёт, например, к неправильной заливки области в графическом редакторе.
Свойства
Пусть нам дано множество отрезков , тогда полученный после выравнивания планарный граф должен обладать следующими свойствами:
- Фиксированная точность координат: все координаты должны лежать в узлах некоторой решётки с шагом .
- Геометрическое подобие: должен полностью лежать в области, полученной суммой Минковского и квадрата со стороной .
- Топологическое подобие: Существует непрерывное преобразование в .
Алгоритм
| Определение: |
| Активная ячейка — ячейка решётки, относительно которой идёт выравнивание, в которую попал конец отрезка или точка пересечения отрезков из . |
| Определение: |
| Пучок — подмножество отрезков , у которых меньший в лексикографическом порядке конец лежит в ячейке . |
| Определение: |
| — отрезок лежащий выше всех в пучке . — отрезок лежащий ниже всех в пучке . |
В целом алгоритм выравнивания похож на алгоритм Бентли-Оттмана, только мы будем манипулировать пучками вместо отрезков.
Инициализируем приоритетную очередь для хранения активных ячеек в лексикографическом порядке. Также инициализируем статус для хранения пучков, которые в данный момент пересекает заметающая прямая. Для каждого конца отрезка из добавим в соответствующую активную ячейку.
Далее будем доставать из активные ячейки и для каждой ячейки выполнять следующие операции:
- Найдём все пучки в статусе , которые пересекают ячейку .
- Разобьём каждый пересекающий пучок на три части:
- Обновим статус.
Упрощение выравнивания
Замечания
Ссылки
- CGAL - 2D Snap Rounding
- Iterated snap rounding with bounded drift
- Efficient Snap Rounding with Integer Arithmetic
- An Intersection-Sensitive Algorithm for Snap Rounding