Моноид
Версия от 02:29, 8 ноября 2013; Shersh (обсуждение | вклад) (добавлено неформальное определение свободного моноида)
| Определение: |
Тройка называется моноидом, если она удовлетворяет следующим аксиомам:
|
Другими словами, моноид — это полугруппа, в которую добавлен нейтральный элемент. Например, множество натуральных чисел с операцией сложения не является моноидом, а с операцией умножения является.
| Утверждение (О единственности нейтрального элемента): |
Нейтральный элемент в моноиде единственен. |
| Действительно, пусть и — два нейтральных элемента. Тогда имеем: . |
| Определение: |
| Свободным моноидом (англ. free monoid) над множеством называется моноид над множеством — набором всевозможных последовательностей (или цепочек) конечной длины (или даже нулевой) из множества . |
| Определение: |
| Гомоморфизмом моноидов (англ. monoid homomorphism) и называется отображение совместимое с операциями из и такое, что , а также . |
| Определение: |
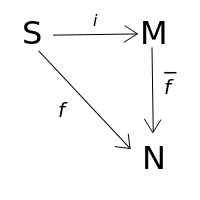
| Свободным моноидом над множеством называется моноид вместе с отображением при условии, что для любого моноида и для любых отображений существует единственный гомоморфизм моноидов такой, что . |
Это наглядно показано следующей картинкой.
Если является подмножеством , то отображение называют естественным вложением (англ. natural injection), и пишут .