Участник:SkudarnovYaroslav/Теормин к зачёту по теории сложности

Определения

Класс P

Определение:

Класс [math]\mathrm{P}[/math] — класс языков (задач), разрешимых на детерминированной машине Тьюринга за полиномиальное время, то есть: [math]\mathrm{P} = \bigcup\limits_{p \in poly}DTIME(p(n))[/math].

Итого, язык [math]L[/math] лежит в классе [math]\mathrm{P}[/math] тогда и только тогда, когда существует такая детерминированная машина Тьюринга [math]m[/math], что:

1. [math]m[/math] завершает свою работу за полиномиальное время на любых входных данных;
2. если на вход машине [math]m[/math] подать слово [math]l \in L[/math], то она допустит его;
3. если на вход машине [math]m[/math] подать слово [math]l \not\in L[/math], то она не допустит его.

Класс NP на языке недетерминированных машин и на языке сертификатов

Определение:

[math]\mathrm{NP}=\bigcup\limits_{p(n) \in poly}\mathrm{NTIME}(p(n))[/math].

То есть [math]\mathrm{NP}[/math] — это множество языков, разрешимых недетерминированной программой за полиномиальное время.

Определение:

[math]\mathrm{\Sigma_1}=\{L\bigm|\exists R(x,y)\in \tilde{\mathrm{P}}, p(n) - poly:x\in L\Leftrightarrow\exists y : |y|\le p(|x|), R(x,y)=1\}[/math].

Нестрого говоря, [math]\mathrm{\Sigma_1}[/math] — это множество языков, для которых существует работающая за полиномиальное время детерминированная программа-верификатор [math]R(x,y)[/math], а для каждого слова из языка (и только для слова из языка) можно предъявить сертификат полиномиальной длины, подтверждающий принадлежность слова языку и проверяемый верификатором.

Сведение по Карпу

Определение:

[math]D[/math] — класс языков, распознаваемых программами с некоторыми ограничениями. Тогда обозначим [math]\widetilde{D}[/math] класс вычислимых функций, вычисляемых программами с теми же ограничениями.

Определение:

Язык [math]L_1[/math] [math]\widetilde{D}[/math]-сводится по Карпу к языку [math]L_2[/math] ([math]L_1 \leq_{\widetilde{D}} L_2[/math]), если существует такая функция [math]f[/math] из [math]\widetilde{D}[/math], что [math]x[/math] принадлежит [math]L_1[/math] тогда и только тогда, когда [math]f(x)[/math] принадлежит [math]L_2[/math]: [math] (L_1 \leq_{\widetilde{D}} L_2) \overset{\underset{\mathrm{def}}{}}{\iff} ( \exists f \in \widetilde{D} : x \in L_1 \Leftrightarrow f(x) \in L_2 ) [/math].

Видимо, это про NP-полные задачи

Определение:

[math]C[/math] — сложностный класс, [math]\widetilde{D}[/math] — класс вычислимых функций. Язык [math]L[/math] называется [math]C[/math]-трудным относительно [math]\widetilde{D}[/math]-сведения ([math]C[/math]-hard), если любой язык [math]M[/math] из [math]C[/math] [math]\widetilde{D}[/math]-сводится к [math]L[/math]: [math] (L [/math] — [math]C[/math]-hard [math]) \overset{\underset{\mathrm{def}}{}}{\Leftrightarrow} ( \forall M \in C \Rightarrow M \leq_{f} L, f \in \widetilde{D} ) [/math].

Определение:

[math]C[/math] — сложностный класс, [math]\widetilde{D}[/math] — класс вычислимых функций. Язык [math]L[/math] называется [math]C[/math]-полным относительно [math]\widetilde{D}[/math]-сведения ([math]C[/math]-complete), если [math]L[/math] является [math]C[/math]-трудным относительно [math]\widetilde{D}[/math]-сведения и сам лежит в [math]C[/math].

Замечание. Часто используется сведение из [math]\widetilde{P}[/math], поэтому вместо «[math]\widetilde{P}[/math]-сводится по Карпу» говорят просто «сводится». Также индекс у символа сведения обычно опускают.

Класс [math]\mathrm{NP}[/math]-полных языков — [math]\mathrm{NPC}[/math]. [math]\mathrm{NPC}[/math] является одним из важнейших классов в теории сложности, так как если найдется язык из этого класса, который также входит в класс [math]\mathrm{P}[/math], тогда окажется, что [math]\mathrm{P} = \mathrm{NP}[/math].

Класс coNP

В теории сложности класс co-NP — класс языков (задач), дополнение к которым лежит в NP.

co-NP = [math]\Pi_1[/math] (См. Полиномиальная иерархия)

Вычисление с оракулом

В теории вычислений и теории сложности "машиной с оракулом" называют абстрактную машину, предназначенную для решения какой-либо проблемы разрешимости. Такая машина может быть представлена как машина Тьюринга, дополненная оракулом с неизвестным внутренним устройством. Постулируется, что оракул способен решить определенные проблемы разрешимости за один такт машины Тьюринга. Машина Тьюринга взаимодействует с оракулом путем записи на свою ленту входных данных для оракула и затем его запуском на исполнение. За один шаг оракул вычисляет функцию, стирает входные данные и пишет выходные данные на ленту. Иногда машина Тьюринга описывается как имеющая две ленты, одна предназначена для входных данных оракула, другая — для выходных.

Определение:

Оракул — абстракция, вычисляющая за [math]O(1)[/math] времени, верно ли, что [math]x[/math] принадлежит множеству [math]A[/math].

Сложностный класс задач, решаемых алгоритмом из класса [math]\mathrm{C}[/math] с оракулом для языка [math]\mathrm{A}[/math], обозначают [math]\mathrm{C^A}[/math].

Класс PS

Определение:

[math]\mathrm{PS}[/math] [math]\mathrm{(PSPACE)}[/math] — класс языков, разрешимых на детерминированной машине Тьюринга с использованием памяти полиномиального размера. [math]\mathrm{PS}=\bigcup\limits_{p(n) \in poly} \mathrm{DSPACE}(p(n))[/math].

Если [math]\mathrm{A}[/math] — множество языков, то [math]\mathrm{C^A} =\bigcup\limits_{D \in A}\mathrm{C^D}[/math].

PS-полная задача

Видимо, тут.

Класс L

Определение:

Класс [math]\mathrm{L}[/math] — множество языков, разрешимых на детерминированной машине Тьюринга с использованием [math]O(\log n)[/math] дополнительной памяти для входа длиной [math]n[/math]. [math]\mathrm{L} = \mathrm{DSPACE}(\log n)[/math].

Класс NL

Определение:

Класс [math]\mathrm{NL}[/math] — множество языков, разрешимых на недетерминированной машине Тьюринга с использованием [math]O(\log n)[/math] дополнительной памяти для входа длиной [math]n[/math]. [math]\mathrm{NL} = \mathrm{NSPACE}(\log n)[/math].

NL-полная задача

Опять же, тут.

Класс P/poly

Определение:

[math] \mathrm{PSIZE} [/math] — класс языков, разрешимых семейством логических схем [math] \{C_n\}_{n\gt 0} [/math] полиномиального размера с n входами и одним выходом. [math] \mathrm{PSIZE} =\{L \bigm| \forall n [/math] [math] \exists C_n [/math]: [math] |C_n| \leqslant p(n)[/math], где [math] p [/math] — полином; Число входов в схеме [math] C_n [/math] равно [math] n [/math]; Каждая схема [math] C_n [/math] имеет один выход; [math]x \in L \Leftrightarrow C_{|x|}(x) = 1 \}[/math].

Определение:

Пусть [math] \mathrm{C} [/math] — сложностный класс, [math] f [/math] — функция. Тогда [math] \mathrm{C}/f = \{L \bigm| [/math] существуют подсказки [math] a_0, a_1, \ldots , a_n, \ldots [/math] и программа [math] p [/math], удовлетворяющая ограничениям [math] \mathrm{C} [/math]: [math]|a_i| \leqslant f(i) [/math]; [math] x \in L \Leftrightarrow p(x, a_{|x|})=1 \}[/math].

Определение:

[math] \mathrm{P/poly} = \bigcup\limits_{p \in poly} \mathrm{P}/p [/math].

Вероятностные вычисления (неформальненько как-то, ну да ладно)

Вероятностные вычисления — один из подходов в теории вычислительной сложности, в котором программы получают доступ, говоря неформально, к генератору случайных чисел. Мы рассмотрим классы сложности, для которых программы могут работать за полиномиальное время и делать односторонние, двусторонние ошибки или работать за полиномиальное время лишь в среднем случае.

Определение:

Вероятностная лента — бесконечная в одну сторону последовательность битов, распределение которых подчиняется некоторому вероятностному закону (обычно считают, что биты в различных позициях независимы и вероятность нахождения [math]0[/math] или [math]1[/math] в каждой позиции равна [math]1/2[/math]).

Определение:

Вероятностная машина Тьюринга (ВМТ) — детерминированная машина Тьюринга, имеющая вероятностную ленту. Переходы в ВМТ могут осуществляться с учетом информации, считанной с вероятностной ленты.

Используя тезис Черча-Тьюринга, ВМТ можно сопоставить программы, имеющие доступ к случайным битам. Обращение к очередному биту можно трактовать как вызов специальной функции random(). При этом также будем предполагать, что вероятностная лента является неявным аргументом программы или ВМТ, т.е. [math]p(x) = p(x, r)[/math], где [math]r[/math] — вероятностная лента.

Класс BPP

Определение:

[math]\mathrm{BPP}[/math] (от bounded probabilistic polynomial) — множество языков [math]L[/math], для которых существует такая ВМТ [math]p[/math], что для любого [math]x[/math]: [math]P(p(x) = [x \in L]) \ge 2/3[/math]; [math]T(p, x) \le poly(|x|)[/math] для любой вероятностной ленты.

[math]\mathrm{BPP}[/math] — сложностный класс, допускающий двусторонние ошибки. Константу [math]2/3[/math] можно заменить на любое число из промежутка [math](1/2, 1)[/math], так как требуемой вероятности можно добиться множественным запуском [math]p[/math]. Замена константы на [math]1/2[/math] сделала бы данный класс равным [math]\Sigma^*[/math] (программа, возвращающая результат функции random(), подошла бы для любого языка).

Класс RP

Определение:

Сложностный класс [math]\mathrm{RP}[/math] состоит из языков [math]L[/math] таких, что существует ВМТ [math]m[/math] такая, что для любого [math]x[/math]: [math]x \notin L \Rightarrow P(m(x) = 0) = 1[/math]; [math]x \in L \Rightarrow P(m(x) = 1) \geq \frac{1}{2}[/math]; [math]T(m(x, r)) \le poly(|x|)[/math] для любой вероятностной ленты [math]r[/math].

[math]\mathrm{RP}[/math] — сложностный класс, допускающий ошибки программ на словах из [math]L[/math]. Заметим, что константа [math]1/2[/math] в пункте 2 определения [math]\mathrm{RP}[/math] может быть заменена на любую другую из промежутка [math](0, 1)[/math], поскольку требуемой вероятности можно добиться множественным запуском программы.

[math]\mathrm{RP}[/math] можно рассматривать как вероятностный аналог класса [math]\mathrm{NP}[/math], предполагая, что вероятность угадать сертификат в случае его существования не менее [math]1/2[/math].

Класс ZPP

Определение:

[math]\mathrm{ZPP}[/math] (от zero-error probabilistic polynomial) — множество языков [math]L[/math], для которых [math]\exists p \forall x[/math]: [math]\operatorname{P}(p(x) \ne [x \in L]) = 0[/math]; [math]\operatorname{E}[\operatorname{T}(p, x)] = poly(|x|)[/math].

[math]\mathrm{ZPP}[/math] — сложностный класс, такой что программы, удовлетворяющие его ограничениям, не могут делать ошибок, но работают за полиномиальное время только в среднем случае.

Напомним, что математическое ожидание является усреднением по вероятностным лентам, а не по входу [math]x[/math].

Интерактивное доказательство (кажется, оно, но не уверен)

Определение:

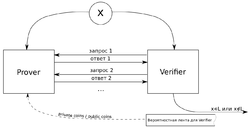
Интерактивным протоколом, разрешающим язык [math]L[/math], называется абстрактная машина (см. рисунок), моделирующая вычисления как обмен сообщениями между двумя программами ([math]\mathit{Prover}[/math] и [math]\mathit{Verifier}[/math]), такими, что [math]\mathit{Prover}[/math] заинтересован в том, чтобы [math]\mathit{Verifier}[/math] решил, что слово [math]x[/math] принадлежит языку; [math]\mathit{Prover}[/math] не ограничен в вычислительной мощности; [math]\mathit{Verifier}[/math] заинтересован установить, действительно ли слово [math]x[/math] принадлежит языку; [math]\mathit{Verifier}[/math] — вероятностная машина Тьюринга; [math]\mathit{Verifier}[/math] ограничен полиномиальным временем работы.

Схема интерактивного протокола.

[math]\mathit{Verifier}[/math], обменивающийся сообщениями с [math]\mathit{Prover}[/math], будем обозначать [math]\mathit{Verifier^{Prover}}[/math].

Интерактивные протоколы делятся на два типа в зависимости от доступа [math]\mathit{Prover}[/math] к вероятностной ленте [math]\mathit{Verifier}[/math]:

1. public coins — [math]\mathit{Prover}[/math] может видеть вероятностную ленту [math]\mathit{Verifier}[/math];
2. private coins — [math]\mathit{Prover}[/math] не может видеть вероятностную ленту [math]\mathit{Verifier}[/math].

Класс IP

Определение:

[math]\mathrm{IP}[f] = \{L\bigm|\exists \langle \mathit{Verifier}, \mathit{Prover} \rangle : [/math] [math]\mathit{Prover}[/math] не имеет доступа к вероятностной ленте [math]\mathit{Verifier}[/math] (private coins); [math] \forall x \in L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) \ge \frac{2}{3} [/math]; [math] \forall x \notin L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) \le \frac{1}{3} [/math]; число раундов интерактивного протокола [math] O(f(n)), n = |x|\}[/math].

Определение:

[math]\mathrm{IP}=\bigcup\limits_{p(n) \in poly} \mathrm{IP} [p(n)] [/math]

Класс AM

Язык [math]\mathrm{AM}[/math] (Arthur–Merlin games) отличается от [math]\mathrm{IP}[/math] лишь тем, что [math]\mathit{Prover}[/math] может видеть вероятностную ленту [math]\mathit{Verifier}[/math].

Определение:

[math]\mathrm{AM}[f] = \{L\bigm|\exists \langle \mathit{Verifier}, \mathit{Prover} \rangle : [/math] [math]\mathit{Prover}[/math] может читать вероятностную ленту [math]\mathit{Verifier}[/math] (public coins); [math] \forall x \in L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) \ge \frac{2}{3} [/math]; [math] \forall x \notin L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) \le \frac{1}{3} [/math]; число раундов интерактивного протокола [math] O(f(n)), n = |x|\} [/math].

Определение:

[math]\mathrm{AM}=\bigcup\limits_{p(n) \in poly} \mathrm{AM} [p(n)] [/math]

Класс PCP

PCP(probabilistically checkable proof) - вид доказательства, проверяемого рандомизированным алгоритмом, использующим ограниченное число случайных бит и читающим ограниченное число бит доказательства. Такой алгоритм должен с достаточно высокими вероятностями принимать корректные доказательства и отвергать ошибочные.

Определение:

[math]\mathrm{PCP}[/math]-системой (системой вероятностно проверяемых доказательств) с полнотой [math]c(n)[/math] и обоснованностью [math]s(n)[/math] над алфавитом [math]\Sigma[/math] для языка [math]L[/math], где [math]0 \le s(n) \le c(n) \le 1[/math], называется верификатор [math]V[/math] — вероятностная машина Тьюринга, имеющая доступ к доказательству [math]\pi[/math] — цепочке из [math]\Sigma^{*}[/math], удовлетворяющая следующим свойствам: Полнота: если [math]x \in L[/math], то вероятность того, что [math]V^{\pi}[/math] допустит [math]x[/math], не меньше [math]c(n)[/math] для некоторого [math]\pi[/math], Обоснованность: если [math]x \notin L[/math], то вероятность того, что [math]V^{\pi}[/math] допустит [math]x[/math], не больше [math]s(n)[/math] для любого [math]\pi[/math].

Определение:

Randomness complexity (вероятностной сложностью) [math]r(n)[/math] верификатора [math]V[/math] называется число случайных битов, используемых за всё время работы со входом длины [math]n[/math].

Определение:

Query complexity (запросной сложностью) [math]q(n)[/math] верификатора [math]V[/math] называется число запросов битов из [math]\pi[/math], отсылаемых за всё время работы со входом длины [math]n[/math].

Определение:

Верификатор [math]V[/math] называется non-adaptive (неадаптивным), если при отправке запроса не использует ответы на предыдущие. Иными словами, его работа не изменится, если все запросы отправить одновременно.

Определение:

Сложностный класс [math]\mathrm{PCP}_{c(n), s(n)}[r(n), q(n)][/math] — это объединение всех языков, для которых существует [math]\mathrm{PCP}[/math]-система над бинарным алфавитом с полнотой [math]c(n)[/math] и обоснованностью [math]s(n)[/math], в которой неадаптивный верификатор [math]V[/math] работает за полиномиальное время и имеет вероятностную и запросную сложности соответственно [math]r(n)[/math] и [math]q(n)[/math], а доказательства имеют экспоненциальную длину. Часто [math]\mathrm{PCP}_{1, \frac{1}{2}}[r(n), q(n)][/math] обозначают как [math]\mathrm{PCP}[r(n), q(n)][/math].