Заданы две окружности разного радиуса точками центров
[math](x_0;y_0)[/math],
[math](x_1;y_1)[/math] и радиусами
[math]r_0[/math] и
[math]r_1[/math] соответственно.
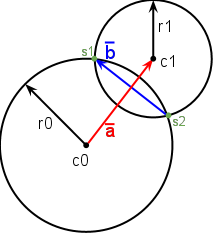
Будем вычислять координаты искомых точек пересечения окружностей в новой системе координат, связанной с векторами [math]\bar{a}[/math] и [math]\bar{b}[/math], которые изображены на рисунке. Искать соответственно будем в виду [math]\alpha\bar{a}+\beta\bar{b}[/math].
Для начала напишем, чему равен вектор [math]\bar{a}=\begin{pmatrix}
x_1-x_0\\
y_1-y_0\\
\end{pmatrix}[/math], вектор [math]\bar{b}[/math] перпендикулярен [math]\bar{a}[/math], следовательно равен [math]\bar{b}=\begin{pmatrix}
-y_1+y_0\\
x_1-x_0\\
\end{pmatrix}[/math].
Коэффициенты [math]\alpha[/math] и [math]\beta[/math] будем искать из системы уравнений [math]\left\{\begin{array}{lrl}
(\alpha\bar{a}+\beta\bar{b})^2=r_0^2\\
(\alpha\bar{a}+\beta\bar{b}-\bar{a})^2=r_1^2\\
\end{array}
\right.[/math]
[math]\left\{\begin{array}{lrl}
\alpha^2\bar{a}^2+\beta^2\bar{b}^2+2\alpha\beta\bar{a}\bar{b}=r_0^2\ \ \ (1)\\
((\alpha-1)\bar{a}+\beta\bar{b})^2=r_1^2\\
\end{array}
\right.[/math]
Заметим, что в уравнении [math](1)[/math] третье слагаемое в правой части равно [math]0[/math], т.к. векторы [math]\bar{a}[/math] и [math]\bar{b}[/math] перпендикулярны.
[math]\left\{\begin{array}{lrl}
\alpha^2\bar{a}^2+\beta^2\bar{b}^2=r_0^2\\
(\alpha-1)^2\bar{a}^2+\beta^2\bar{b}^2=r_1^2\\
\end{array}
\right.[/math]
[math]\left\{\begin{array}{lrl}
2\alpha-1=\frac{r_0^2-r_1^2}{\bar{a}^2}\\
\beta^2\bar{b}^2=r_0^2-\alpha^2\bar{a}^2\\
\end{array}
\right.[/math]
[math]\left\{\begin{array}{lrl}
\alpha=\frac{r_0^2-r_1^2+\bar{a}^2}{2\bar{a}^2}\\
\beta^2\bar{b}^2=r_0^2-\alpha^2\bar{a}^2\\
\end{array}
\right.[/math]
[math]\left\{\begin{array}{lrl}
\alpha=\frac{r_0^2-r_1^2+\bar{a}^2}{2\bar{a}^2}\\
\beta^2=\frac{r_0^2-\frac{(r_0^2-r_1^2+\bar{a}^2)^2}{4\bar{a}^4}\bar{a}^2}{\bar{b}^2}\\
\end{array}
\right.[/math]
[math]\left\{\begin{array}{lrl}
\alpha=\frac{r_0^2-r_1^2+\bar{a}^2}{2\bar{a}^2}\\
\beta=\pm\frac{1}{|\bar{a}||\bar{b}|}\sqrt{-\frac{1}{2}(r_0^4+r_1^4+\bar{a}^4-2r_0^2r_1^2-2r_1^2\bar{a}^2)}\\
\end{array}
\right.[/math]
Мы, например, будем рассматривать точку с положительным знаком [math]\beta[/math].
Радиус-вектор такой точки будет равен [math]\bar{s_1}=\bar{c_0}+\alpha\bar{a}+\beta\bar{b}[/math].
