Интерактивные протоколы. Класс IP. Класс AM

Материал из Викиконспекты
Перейти к: навигация, поиск
НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.

Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.

Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.

Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.

Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Определения

Определение:
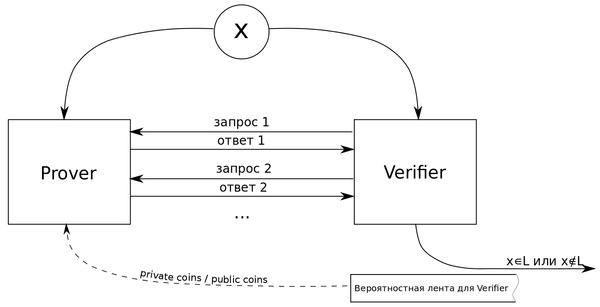
Интерактивным протоколом (англ. interactive protocol) [math] \langle P, V \rangle [/math], разрешающим язык [math]L[/math], называется абстрактная машина (см. рисунок), моделирующая вычисления как обмен сообщениями между двумя программами (где [math]P[/math] означает [math] \mathrm{Prover}[/math] и [math] V [/math] означает [math]\mathrm{Verifier}[/math]), такими, что
  1. [math]P[/math] заинтересован в том, чтобы [math]V[/math] решил, что слово [math]x[/math] принадлежит языку.
  2. [math]P[/math] не ограничен по времени вычисления и памяти.
  3. [math]V[/math] заинтересован установить, действительно ли слово [math]x[/math] принадлежит языку.
  4. [math]V[/math] — вероятностная машина Тьюринга.
  5. [math]V[/math] ограничен полиномиальным временем работы.
Схема интерактивного протокола.

Замечания:

  1. [math] V [/math] и [math] P [/math] по очереди становятся активными. [math] V [/math] активизируется первым. В течение работы [math] V [/math] выполняет вычисления, используя вход, очередные данные с вероятностной ленты и сообщение, пришедшее от [math] P [/math], и пишет запрос [math] P [/math]. Как только [math] V [/math] написал сообщение, он дизактивируется, и [math] P [/math] становится активным, если протокол не завершился. Любая машина может завершить выполнение протокола просто не посылая сообщение во время своей активной фазы. [math] V [/math] принимает (или отвергает) вход, выводит true (или false) и завершает выполнение протокола. Время работы [math] V [/math] — это сумма времен работы, затраченных [math] V [/math] в течение активной фазы, и это время ограничено полиномом от длины входа.
  2. [math]V[/math], обменивающийся сообщениями с фиксированным [math]P[/math], обозначим [math]V_{P}[/math].
  3. Для того, чтобы [math] V [/math] принял слово, [math]P[/math] старается максимизировать вероятность [math]\mathbb{P}(V_{P}(x) = 1)[/math], выбирая нужные ответы на запросы.
  4. Так как мы не ограничиваем [math]P[/math] в вычислительной мощности, то он может работать бесконечное время, а значит [math]V[/math] не получит ответ на какой-то вопрос. Но [math]P[/math] хочет, чтобы [math] V[/math] принял слово, значит нужно выбирать "хорошие" протоколы, чтобы таких ситуаций не появлялось.
  5. [math] P [/math] может быть и вероятностной и детерминированной машиной Тьюринга. Так как он имеет неограниченные вычислительные ресурсы, то на каждом ходу он может выбрать такие вероятностные данные и произвести вычисления с ними, что они максимизируют вероятность принятия слова [math] V [/math].
  6. С другой стороны, для [math] V [/math] важно быть вероятностной программой, так как иначе он будет принимать или отвергать слова с вероятностью [math] 1 [/math]. И пользуясь предыдущим фактом, получим, что [math] V_{P} [/math] всегда принимает слова из [math] L [/math].
  7. Так как [math] V [/math] может писать и читать полиномиальное число символов, то длина сообщений между [math] V [/math] и [math] P [/math] есть полином от длины [math] x [/math].

Интерактивные протоколы делятся на два типа в зависимости от доступа [math]P[/math] к вероятностной ленте [math]V[/math]:

  1. public coins (русск. открытые монеты) — [math]P[/math] может видеть вероятностную ленту [math]V[/math];
  2. private coins (русск. закрытые монеты)— [math]P[/math] не может видеть вероятностную ленту [math]V[/math].


Определение:
Если для интерактивного протокола выполняется [math] \forall x \in L \Rightarrow \exists P : \mathbb{P}(V_{P}(x) = 1) \geqslant c [/math], то говорят, что он обладает свойством completeness (русск. полнота) равным [math] c [/math].

Если [math]c = 1[/math] (perfect completeness (русск. идеальная полнота)), то это означает, что никакое верное утверждение не отклоняется [math] V [/math].


Определение:
Если для интерактивного протокола выполняется [math] \forall x \notin L \Rightarrow \forall P : \mathbb{P}(V_{P}(x) = 1) \leqslant 1 - s [/math], то говорят, что он обладает свойством soundness (русск. достоверность) равным [math] s [/math].

Если [math]s = 1 [/math] (perfect soundness (русск. идеальная достоверность)), то это означет, что если утверждение ложно, то никакой [math]P[/math] не может убедить [math]V[/math], что утверждение истино. В этом случае мы получем класс [math] \mathrm{NP} [/math]. Потому что [math] x \in L [/math] тогда и только тогда, если существует последовательность случайных вопросов, генерируемых [math] V [/math], и последовательность ответов [math] P [/math], которые убеждают [math] V [/math] в том, что [math] x \in L [/math]. Обратное утверждение сохраняется по предположению идеальной достоверности.


Определение:
[math]\mathrm{IP}[f] [/math] (Interactive Polynomial time) [math] = \{L \mid \exists [/math] интерактивный протокол [math]\langle P, V \rangle : [/math]
  1. [math]P[/math] не имеет доступа к вероятностной ленте [math]V[/math] (private coins).
  2. [math] c \geqslant 2/{3} [/math].
  3. [math] s \geqslant 2 /{3} [/math].
  4. число раундов интерактивного протокола [math] O(f(n)), n = |x|\}[/math].


Определение:
[math]\mathrm{IP}=\bigcup\limits_{p(n) \in poly} \mathrm{IP} [p(n)] [/math]

То есть [math] \mathrm{IP}[/math] — множество языков разрешимых интерактивным протоколом, таких, что число сообщений ограничено полиномом от длины слова и [math]V[/math] должен решить лежит ли слово в языке с вероятностью ошибки не более [math]1/{3}[/math].

Язык [math]\mathrm{AM}[/math] (Arthur–Merlin games) отличается от [math]\mathrm{IP}[/math] лишь тем, что [math]P[/math] может видеть вероятностную ленту [math]V[/math].

Определение:
[math]\mathrm{AM}[f] = \{L \mid \exists [/math] интерактивный протокол [math]\langle P, V \rangle : [/math]
  1. [math]P[/math] может читать вероятностную ленту [math]V[/math] (public coins).
  2. [math] c \geqslant 2/{3} [/math].
  3. [math] s \geqslant 2 /{3} [/math].
  4. число раундов интерактивного протокола [math] O(f(n)), n = |x|\}[/math].


Определение:
[math]\mathrm{AM}=\bigcup\limits_{p(n) \in poly} \mathrm{AM} [p(n)] [/math]


Соотношения с другими классами теории сложности

Теорема:
[math]\mathrm{BPP}[/math] [math]\subset \mathrm{IP}[0][/math].
Доказательство:
[math]\triangleright[/math]
[math]V[/math] сам по себе является вероятностной машиной Тьюринга и поэтому может разрешить язык из [math]\mathrm{BPP}[/math] не прибегая к общению с [math]P[/math].
[math]\triangleleft[/math]
Теорема:
[math]\mathrm{NP} \subset \mathrm{IP}[1][/math].
Доказательство:
[math]\triangleright[/math]

Для разрешения языка из [math]\mathrm{NP}[/math] будем использовать следующий протокол:

[math]V[/math] будет проверять на принадлежность слова [math]x[/math] языку, используя сертификат, который он запросит у [math]P[/math]. Так как [math]P[/math] не ограничен в вычислительной мощности, он может подобрать подходящий сертификат и именно его и сообщит, так как он заинтересован в том, чтобы [math]V[/math] принял слово. Для этого требуется лишь один раунд интерактивного протокола.
[math]\triangleleft[/math]

Язык GNI

Определение:
[math]\mathrm{GNI}[/math] расшифровывается как Graph Non Isomorphism. Это язык пар неизоморфных друг другу графов. [math]\mathrm{GNI}=\{ \langle G, H \rangle \mid [/math] графы [math]G[/math] и [math]H[/math] не изоморфны [math]\}[/math].


Теорема:
[math]\mathrm{GNI} \in \mathrm{IP}[1][/math].
Доказательство:
[math]\triangleright[/math]

Пусть на вход подали пару графов [math] \langle G_{0}, G_{1} \rangle [/math] и нужно определить изоморфны ли они. Будем использовать следующий алгоритм для [math]V[/math]:

  1. Возьмём случайное число [math]i \in \{0, 1\}[/math] и случайную перестановку [math]\pi[/math] с вероятностной ленты;
  2. Создадим новый граф [math] G [/math], перемешав вершины графа c номером [math]i[/math] перестановкой [math]\pi[/math].
  3. Перешлём [math]P[/math] полученный граф [math] G [/math] с просьбой определить, из какого из исходных графов он был получен. Если [math]G_{0} \ncong G_{1} [/math], то он может перебрать все перестановки графов [math] G_{0}, G_{1} [/math], и так как [math]G_{0} \ncong G_{1} [/math], то только одна перестановка только на одном графе даст [math] G [/math]. Иначе, существуют такие перестановки [math] \phi, \psi [/math], что [math] \phi(G_0) = \psi(G_1) = G [/math], и [math] P [/math] никак не сможет определить из какого графа был получен [math] G [/math]. Тогда [math] P [/math] просто попытается угадать граф, вернув случайно [math] 0 [/math] или [math] 1 [/math].
  4. Получив ответ, сравним его с правильным ответом — числом [math]i[/math].
  5. Если полученный ответ не совпадёт с [math]i[/math], то вернём [math]0[/math].
  6. Иначе повторим первые пять шагов ещё раз и перейдём к последнему шагу.
  7. Если мы ещё не вернули [math]0[/math], то вернём [math]1[/math].

Покажем, что это удовлетворяет ограничениям на [math]\mathrm{IP}[1][/math]. Во-первых, очевидно, что число раундов не превосходит двух.

Рассмотрим теперь два случая:

  • [math] \langle G, H \rangle \in \mathrm{GNI}[/math]. Тогда [math]G[/math] и [math]H[/math] неизоморфны и [math]P[/math] сможет определить какой граф был перемешан [math]V[/math]. Таким образом, [math]P[/math] сможет два раза подряд вернуть правильный ответ и в итоге [math]V[/math] вернёт [math]1[/math]. То есть получили completeness равную [math] 1 [/math].
  • [math] \langle G, H \rangle \notin \mathrm{GNI}[/math]. Тогда [math]G[/math] и [math]H[/math] изоморфны и [math]P[/math] не сможет определить какой граф был перемешан [math]V[/math]. Так как [math]P[/math] заинтересован в том, чтобы [math]V[/math] принял слово, ему необходимо угадать правильный ответ (иначе [math]V[/math] просто вернёт [math]0[/math]). Вероятность того, что [math]V[/math] примет слово [math]x[/math], когда оно не принадлежит языку (то есть [math]P[/math] два раза подряд верно угадает номер графа с вероятностью [math] 0.5 [/math]), равна [math]0.25[/math]. Значит soundness равна [math] 0.75 [/math], что больше или равно [math] 2/{3} [/math].
Таким образом, построенный протокол удовлетворяет условию теоремы.
[math]\triangleleft[/math]

См. также

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Интерактивные_протоколы._Класс_IP._Класс_AM&oldid=83175»