Матрица Кирхгофа
Версия от 08:00, 3 февраля 2012; Igor buzhinsky (обсуждение | вклад) (→Определение матрицы Кирхгофа)
Содержание
Определение матрицы Кирхгофа
| Определение: |
| Матрицей Кирхгофа простого графа называется матрица , элементы которой определяются равенством: |
Иными словами, на главной диагонали матрицы Кирхгофа находятся степени вершин, а на пересечении -й строки и -го столбца () стоит -1, если вершины с номерами и смежны, и 0 в противном случае.
Пример матрицы Кирхгофа
| Граф | Матрица Кирхгофа |
|---|---|
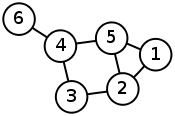
|
Некоторые свойства
1) Матрица Кирхгофа является симметрической (т.е. симметрична относительно главной диагонали).
2) Связь с матрицей смежности:
где — матрица смежности графа .
3) Связь с матрицей инцидентности: где — матрица инцидентности некоторой ориентации графа.
Источники
Асанов М., Баранский В., Расин В. — Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр.
Википедия, Матрица Кирхгофа