Локальные автоматы

Описание

Определение:

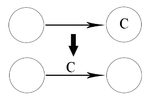
Граф Майхилла [math]G[/math] (над алфавитом [math]\Sigma[/math]) (англ. Myhill graph) — ориентированный граф, удовлетворяющий свойствам: Для каждой упорядоченной пары вершин [math]v[/math] и [math]u[/math] существует только одно ребро из [math]v[/math] в [math]u[/math]. Некоторые вершины обозначены начальными, а некоторые — конечными. Ребро может одновременно быть начальным и конечным. Вершины обозначены различными символами из конечного алфавита [math]\Sigma[/math], то есть мы можем обращаться к вершине по ее символу.

Пусть [math]G[/math] — граф Майхилла над алфавитом [math]\Sigma[/math].

Символ [math]c \in \Sigma[/math] назовем разрешенным, если им помечена вершина, являющая одновременно начальной и конечной.

Не пустая строка [math]c_1c_2 \ldots c_n[/math] из [math]\Sigma^*[/math] длиной не менее двух символов, называется разрешенной, если символом [math]c_1[/math] отмечена стартовая вершина, а символом [math]c_n[/math] — конечная, и для всех [math]1 \leqslant i \leqslant n - 1[/math] в [math]G[/math] существует ребро [math](c_i, c_{i+1})[/math].

Язык [math]L(G)[/math], распознаваемый графом Майхилла, состоит из всех разрешенных строк из [math]\Sigma^+[/math].

Покажем, что графы Майхилла могут быть представлены в виде автоматов. Пусть [math]\mathcal{A} = (S, \Sigma, i, \delta, T)[/math] — ДКА.

Определение:

Автомат [math]\mathcal{A}[/math] называется локальным (англ. local automaton, Glushkov automaton), если для любого [math]c[/math] из [math]\Sigma[/math] множество [math]\{\delta(s, c) \mid s \in S\}[/math] содержит не более одного элемента.

Определение:

Локальный автомат [math]\mathcal{A}[/math] называется стандартным локальным автоматом (англ. standard local automation), если в нем нет перехода в начальное состояние.

Таким образом, автомат является локальным, если для каждого [math]c[/math] из [math]\Sigma[/math] нет переходов, отмеченных [math]c[/math], или если все они ведут в одно состояние.

Покажем, что граф Майхилла может быть преобразован в стандартный локальный автомат таким образом, что распознаваемый им язык не изменится.

Теорема:

Язык распознается графом Майхилла тогда и только тогда, когда он распознается стандартным локальным автоматом, стартовое состояние которого не является терминальным.

Доказательство:

[math]\triangleright[/math]

[math]\Rightarrow[/math] Пусть [math]G[/math] — граф Майхилла. Построим автомат [math]\mathcal{A}[/math] следующим образом: Добавим вершину [math]\Diamond[/math] в [math]G[/math] с ребрами от [math]\Diamond[/math] к каждой стартовой вершине [math]G[/math]; отметим вершину [math]\Diamond[/math] как стартовое состояние. Отметим конечные вершины как терминальные состояния. Отметим каждое ребро результирующего ориентированного графа символом, стоящим в вершине, на которою оно указывает. Переходы преобразуются следующим образом: По построению стартовое состояние не является терминальным. Покажем, что полученный автомат конечен. Ребра, выходящие из стартового состояния обозначены различными символами, потому что они указывают на вершины, которые, по свойству 3, были отмечены различными символами в исходном автомате. Если мы рассмотрим любое другое состояние [math]s[/math], то два перехода из [math]s[/math] могут иметь одинаковые метки только в том случае, если в [math]G[/math] оба ориентированных ребра идут в одну и ту же вершину. Но этого не может быть по свойтсву 1. То есть [math]\mathcal{A}[/math] — ДКА. По построению он является стандартным локальным автоматом. Теперь просто проверить, что [math]L(\mathcal{A}) = L(G)[/math]. [math]\Leftarrow[/math] Пусть [math]\mathcal{A} = (S, \Sigma, i, \delta, T)[/math] — стандартный локальный автомат, стартовое состояние которого не является терминальным. Построим по нему граф Майхилла следующим образом: Отметим все состояния [math]\mathcal{A}[/math], кроме стартового, [math]input[/math] символами, стоящими на ребрах, входящих в эти состояния. Сотрем все метки на ребрах [math]\mathcal{A}[/math]. Отметим все состояния [math]s[/math] как начальные вершины, если существует переход из [math]i[/math] в [math]s[/math] Отметим все терминальные состояния как конечные вершины. Удалим вершину [math]i[/math] и все ребра, исходящие из нее. Назовем полученный граф [math]G[/math] — он будет графом Майхилла по построению. Легко проверить, что [math]L(G) = L(\mathcal{A})[/math].

[math]\triangleleft[/math]

Пример

Рисунок 1

Рисунок 2

Граф Майхилла, изображенный на рисунке 1 может быть использован для распознавания строк над алфавитом [math]\Sigma = \{a, b\}[/math]. По определению, язык, распознаваемый данным графом, состоит из непустых строк, начинающихся и заканчивающихся на [math]a[/math].

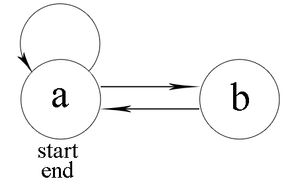
Недетерминированный автомат на рисунке 2 является локальным автоматом и распознает тот же самый язык.

Локальный язык

Рассмотрим язык, распознаваемый стандартным локальным автоматом.

Определение:

Язык [math]L \subseteq A^*[/math] называется локальным языком (англ. local language), если [math]L \setminus \varepsilon[/math] может быть описан следующим образом: [math]\exists P, S \subseteq A, N \subseteq A^2: L \setminus \varepsilon = (P A^* \cap A^* S) \setminus A^* N A^*[/math].

Другими словами, непустое слово принадлежит локальному языку, если оно начинается с символа из [math]P[/math], оканчивается на символ из [math]S[/math] и не содержит пары символов из множества [math]N[/math].

Пусть [math]L = (P A^* \cap A^* S) \setminus A^* N A^*[/math] — локальный язык. Определим автомат [math]\mathcal{A}[/math] следующим образом:

• набор состояний [math]Q = A \cup \{ \varepsilon \}[/math],
• начальное состояние [math]\varepsilon[/math],
• терминальные состояния [math]S[/math],
• [math]\delta(\varepsilon, a) = a[/math] если [math]a \in P[/math] и [math]\delta(a, b) = b[/math] если [math]ab \not\in N[/math].

Если [math]L[/math] содержит пустую строку, то множество терминальных состояний [math]\mathcal{A}[/math] — [math]S \cup \{ \varepsilon \}[/math].

Утверждение:

Определенный таким образом автомат [math]\mathcal{A}[/math] — стандартный локальный автомат, распознающий [math]L[/math].

[math]\triangleright[/math]

Автомат является локальным поскольку для каждого состояния [math]s[/math] и любого символа [math]a[/math] [math]\delta(s, a)[/math] либо неопределена либо равна [math]a[/math]. По построению автомат является стандартным. Покажем, что [math]L(\mathcal{A}) = L[/math]. Пусть [math]x = a_1 \ldots a_n \in L(\mathcal{A})[/math]. Тогда в автомате существует путь: [math]\varepsilon \xrightarrow{a_1} a_1 \xrightarrow{a_2} a_2 \ldots a_{n-1} \xrightarrow{a_n} a_n[/math]. Здесь [math]a_n[/math] — терминальное состояние, [math]a_n \in S[/math]. Переход из [math]\varepsilon[/math] в [math]a_1[/math] определен, поэтому [math]a_1 \in P[/math]. Для каждого [math]j: 1 \leqslant j \leqslant n - 1[/math] факт, что переход [math]a_j \rightarrow a_{j+1}[/math] существует, означает что [math]a_j a_{j+1} \not \in N[/math]. Следовательно, [math]x \in L[/math]. Пусть [math]x = a_1 \ldots a_n \in L[/math]. Тогда [math]a_1 \in P[/math], [math]a_n \in S[/math] и для каждого [math]j[/math] [math]a_j a_{j+1} \not \in N[/math]. Следовательно в автомате существует путь из начального состояния в терминальное: [math]\varepsilon \xrightarrow{a_1} a_1 \xrightarrow{a_2} a_2 \ldots a_{n-1} \xrightarrow{a_n} a_n[/math]. Следовательно, [math]x \in L(\mathcal{A})[/math].

[math]\triangleleft[/math]

Утверждение:

Язык, распознаваемый локальным автоматом, является локальным.

Алгоритм Глушкова

Описание

Дано регулярное выражение [math]e[/math]. Алгоритм Глушкова строит недетерминированный автомат, который распознает язык [math]L(e)[/math], распознаваемый [math]e[/math]. Построение происходит в несколько шагов:

1. Линеаризация регулярного выражения. Каждый символ из алфавита, содержащийся в регулярном выражении, переименовывается таким образом, что каждый символ содержится в новом регулярном выражении не более одного раза. Пусть [math]A[/math] — исходный алфавит, [math]B[/math] — новый алфавит.
2. Вычисление множеств [math]P(e'), S(e'), N(e')[/math], где [math]e'[/math] — линеаризованное регулярное выражение. [math]P(e')[/math] — множество символов, с которых начинается слово из [math]L(e')[/math]. [math]S(e')[/math] — множество символов, на которые оканчивается слово из [math]L(e')[/math] и [math]N(e')[/math] — множество пар символов, которые встречаются в слове из [math]L(e')[/math]. Более формально:
   [math]P(e')=\{a\in B\mid aB^*\cap L(e')\ne\emptyset\}[/math],
   [math]S(e')=\{a\in B\mid B^*a\cap L(e')\ne\emptyset\}[/math],
   [math]N(e')=\{u\in B^2\mid B^*uB^*\cap L(e')\ne\emptyset\}[/math].
3. Вычисление множества [math]\Lambda(e')[/math] такого что [math]\Lambda(e')=\{\varepsilon\}\cap L(e')[/math].
4. Вычисление локального языка с заданными множествами и построение по нему автомата.
5. Делинеаризация, переименование каждого символа из [math]B[/math] в соответствующий ему символ из [math]A[/math].

Пример работы

Автомат, построенный в ходе работы алгоритма Глушкова

Рассмотрим регулярное выражение [math]e = (a(ab)^*)^* + (ba)^*[/math].

1. Линеаризуем его путем добавления индекса к каждому символу:

[math]e'=(a_1(a_2b_3)^*)^*+(b_4a_5)^*[/math].

2. Составим множества [math]P[/math], [math]S[/math], и [math]N[/math]:

[math]P(e')=\{a_1,b_4\}[/math],

[math]S(e')=\{a_1,b_3,a_5\}[/math],

[math]N(e')=\{a_1a_2, a_1a_1, a_2b_3, b_3a_1,b_3a_2,b_4a_5,a_5b_4\}[/math].

Так как пустое слово принадлежит языку, то [math]\Lambda(e')=\{\varepsilon\}[/math].

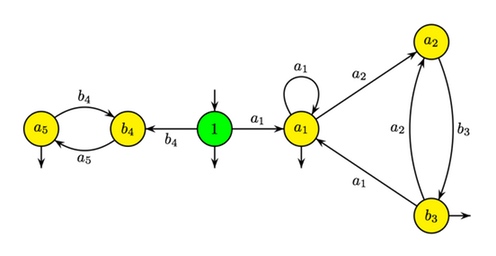
3. Автомат локального языка [math]L'=P'B^*\cap B^*S'\setminus B^*(B^2\setminus N')B^*[/math] содержит начальное состояние, обозначенное как [math]1[/math], и состояния для каждого из пяти символов алфавита [math]B=\{a_1, a_2, b_3, b_4, a_5\}[/math].
В построенном автомате существует переход из [math]1[/math] (соответствующего пустой строке) в два состояния из [math]P'[/math], переход из [math]a[/math] в [math]b[/math] если [math]ab \in N'[/math], три состояния [math]S'[/math] терминальные (как и состояние [math]1[/math]).

4. Получим автомат для [math]L(e)[/math], удалив индексы, добавленные на первом этапе.

См. также

• Контексты и синтаксические моноиды

Источники информации

• Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений
• Mark V. Lawson — Finite Automata
• Wikipedia — Glushkov's construction algorithm