XOR-SAT

Задача:

$\mathrm {XORSAT}$ (XOR-satisfiability) выполнимость функции — задача распределения аргументов в булевой КНФ функции, записанной в виде XOR-КНФ, таким образом, чтобы результат данной функции был равен $1$.

Описание

Одним из особых случаев $\mathrm {SAT}$ является класс задач, где каждый конъюнкт содержит операции $\oplus$ (т. е. исключающее или), а не (обычные) $\lor$ операторы.(Формально, обобщенная КНФ с тернарным булевым оператором $\mathrm {R}$ работает только если $1$ или $3$ переменные дают $\mathtt {true}$ в своих аргументах. Конъюнкты,имеющие более $3$ переменных могут быть преобразованы в сочетании с формулой преобразования с сохранением выполнимости булевой функции, т. е. $\mathrm {XOR}$-$\mathrm {SAT}$ может быть снижена до $\mathrm {XOR}$-$3$-$\mathrm {SAT}$)

Это задача Р-класса, так как $\mathrm {XOR}$-$\mathrm {SAT}$ формулу можно рассматривать как систему линейных уравнений по модулю $2$, которая, в свою очередь, может быть решена за $O(n^3)$ методом Гаусса .Такое представление возможно на основе связи между Булевой алгеброй и Булевым кольцом и том факте, что арифметика по модулю $2$ образует конечное поле .

Решение XOR-SAT задачи методом Гаусса

Система уравнений
("$1$" означает «$\mathtt {true}$», "$0$" означает «$\mathtt {false}$») Каждый конъюнкт ведет к одному уравнению.
Переменные	Значение
$a$ $\oplus$ $c$ $\oplus$ $d$	$=1$
$b$ $\oplus$ $\neg c$ $\oplus$ $d$	$=1$
$a$ $\oplus$ $b$ $\oplus$ $\neg d$	$=1$
$\neg a$ $\oplus$ $\neg b$ $\oplus$ $\neg c$	$=1$
$\neg a$ $\oplus$ $b$ $\oplus$ $c$	$\cong 1$

Нормированная система уравнений
Используя свойства Булевых колец ($\neg x=1 \oplus x$, $x \oplus x=1$)
Переменные	Значение
$a$ $\oplus$ $c$ $\oplus$ $d$	$=1$
$b$ $\oplus$ $c$ $\oplus$ $d$	$=0$
$a$ $\oplus$ $b$ $\oplus$ $d$	$=0$
$a$ $\oplus$ $b$ $\oplus$ $c$	$=1$
$a$ $\oplus$ $b$ $\oplus$ $c$	$\cong 0$

Матрица соответствующих коэффициентов
$a$	$b$	$c$	$d$		Строка
$1$	$0$	$1$	$1$	$1$	$A$
$0$	$1$	$1$	$1$	$0$	$B$
$1$	$1$	$0$	$1$	$0$	$C$
$1$	$1$	$1$	$0$	$1$	$D$

Преобразования, чтобы сформировать верхнюю треугольную матрицу
$a$	$b$	$c$	$d$		Операция
$1$	$0$	$1$	$1$	$1$	$A$
$1$	$1$	$0$	$1$	$0$	$C$
$1$	$1$	$1$	$0$	$1$	$D$
$0$	$1$	$1$	$1$	$0$	$B$

$1$	$0$	$1$	$1$	$1$	$A$
$1$	$1$	$0$	$1$	$0$	$C$
$1$	$1$	$1$	$0$	$1$	$D$
$0$	$1$	$1$	$1$	$0$	$B$

$1$	$0$	$1$	$1$	$1$	$A$
$0$	$1$	$1$	$0$	$1$	$E=C \oplus A$
$0$	$1$	$0$	$1$	$0$	$F=D \oplus A$
$0$	$1$	$1$	$1$	$0$	$B$

$1$	$0$	$1$	$1$	$1$	$A$
$0$	$1$	$1$	$0$	$1$	$E$
$0$	$0$	$1$	$1$	$1$	$G=F \oplus E$
$0$	$0$	$0$	$1$	$1$	$H=B \oplus E$

Преобразования, чтобы сформировать диагональную матрицу
$a$	$b$	$c$	$d$		Операция
$1$	$0$	$1$	$0$	$0$	$I=A \oplus H$
$0$	$1$	$1$	$0$	$1$	$E$
$0$	$0$	$1$	$0$	$0$	$J=G \oplus H$
$0$	$0$	$0$	$1$	$1$	$H$

$1$	$0$	$0$	$0$	$0$	$K=I \oplus J$
$0$	$1$	$0$	$0$	$1$	$L=E \oplus J$
$0$	$0$	$1$	$0$	$0$	$J$
$0$	$0$	$0$	$1$	$1$	$H$

Следствие:$R$($a$,$c$,$d$)$\land$ $R$($b$,$\neg c$,$d$)$\land$$R$($a$,$b$,$\neg d$)$\land$$R$($a$,$\neg b$,$\neg c$)∧ R(¬a,b,c)

Вычислительная сложность

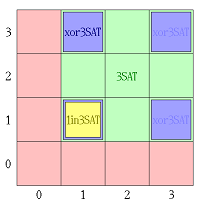
Формула с $2$-мя дизъюнктами может быть неудовлетворена(красный),$3$-$\mathrm {SAT}$(зелёный),$\mathrm {XOR}$-$3$-$\mathrm {SAT}$(синий) ,или/и $1$-$\mathrm {in}$-$3$-$\mathrm {SAT}$, в зависимости от количества переменных со значением $\mathtt {true}$ в $1$-м (горизонтальном) и втором (вертикальном) конъюнкте.

Поскольку $a\ XOR\ b\ XOR\ c$ принимает значение $\mathtt {true}$,если и только если $1$ из $3$ переменных {$a$,$b$,$c$} принимает значение $\mathtt {true}$ ,каждое решение в $1$-$\mathrm {in}$-$3$-$\mathrm {SAT}$ задачи для данной КНФ-формулы является также решением $\mathrm {XOR}$-$3$-$\mathrm {SAT}$ задачи, и ,в свою очередь,обратное также верно.
Как следствие, для каждой КНФ-формулы, можно решить $\mathrm {XOR}$-$3$-$\mathrm {SAT}$-задачу и на основании результатов сделать вывод, что либо $3$-$\mathrm {SAT}$ задача решаема или, что $1$-$\mathrm {in}$-$3$-$\mathrm {SAT}$-задача нерешаема.
При условии ,что P- и NP-классы не равны,ни $2$-,ни Хорн-,ни $\mathrm {XOR}$-$\mathrm {SAT}$ не являются задачи NP-класса,в отличии от $\mathrm {SAT}$.

См. также

• Специальные формы КНФ
• 2SAT
• NP-полнота задачи о выполнимости булевой формулы в форме 3-КНФ

Источники информации

• Википедия — Boolean satisfiability problem
• Cook, Stephen A.Proceedings of the 3rd Annual ACM Symposium on Theory of Computing: 151–158, 1971.