Обсуждение участницы:Анна

Перечисления графов

Помеченные графы

Определение:

Помеченный граф с [math]n[/math] вершинами — граф, у которого каждая вершина помечена целым числом от [math]1[/math] до [math]n[/math].

Более формально определить это понятие можно так: назовем распределением [math]f[/math] меток в графе [math]G[/math] с [math]n[/math] вершинами биекцию между множеством вершин графа и множеством [math]\{1 \cdots n\}[/math]. Тогда помеченным графом называется пара [math](G, f)[/math].

Определение:

Два помеченных графа [math](G_{1}, f_{1})[/math] и [math](G_{2}, f_{2})[/math] изоморфны, если существует изоморфизм между [math]G_{1}[/math] и [math]G_{2}[/math], сохраняющий распределение меток.

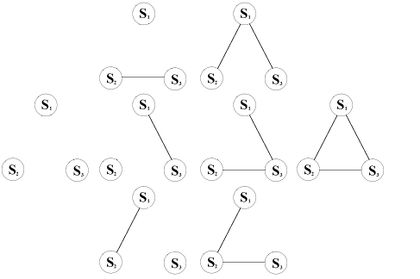
Все помеченные графы с тремя вершинами показаны на рисунке 1. [math]4[/math] различных графа с [math]3[/math] вершинами приводят к [math]8[/math] различным помеченным графам.

Рис. 1. Помеченные графы с тремя вершинами.

Для нахождения числа помеченных графов с [math]p[/math] вершинами нужно заметить, что каждое из [math] p\choose 2[/math] возможных ребер либо принадлежит графу, либо нет.

Теорема (1):

Число помеченных графов с [math]p[/math] вершинами равно [math] 2^{p\choose 2}[/math].

Следовательно, число помеченных графов с [math]q[/math] ребрами равно [math] {p\choose 2}\choose q[/math].

Теорема (Кэли):

Число помеченных деревьев с [math]p[/math] вершинами равно [math] p^{p - 2}[/math].

Теорема (2):

Данный граф [math]G[/math] можно пометить [math]\frac{p!}{|\Gamma(G)|}[/math] способами.

Доказательство:

[math]\triangleright[/math]

Приведем набросок доказательства. Пусть [math]A[/math] — группа подстановок, действующая на множестве [math]X[/math]. Для всякого элемента [math]x \in X[/math] орбитой [math]\Theta(x)[/math] элемента [math]x[/math] называется подмножество множества [math]X[/math], состоящее из всех элементов [math]y \in X[/math] таких, что [math]\alpha \cdot x = y[/math] для некоторой подстановки [math]\alpha[/math] из [math]A[/math]. Стабилизатором [math]A(x)[/math] элемента [math]x[/math] называется подгруппа группы [math]A[/math], состоящая из всех подстановок из [math]A[/math], оставляющих элемент [math]x[/math] неподвижным. Теорема является следствием соотношения [math]|A| = |\Theta(x)|\cdot|A(x)|[/math] и его интерпретации в настоящем контексте.

[math]\triangleleft[/math]

Рис. 2. Помеченные деревья с четырьмя вершинами.

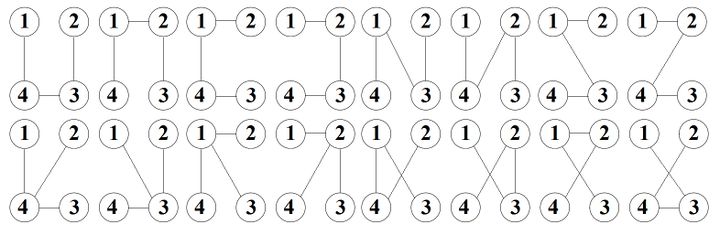
Рассмотрим пример. На рисунке 2 изображены все помеченные деревья с четырьмя вершинами. Всего их [math]16[/math]. Среди них [math]12[/math] изоморфны цепи [math]P_{4}[/math] и [math]4[/math] — графу [math]K_{1, 3}[/math]. Порядок группы [math]\Gamma(P_{4})[/math] равен [math]2[/math]. Порядок группы [math]K_{1, 3} = 6[/math]. Так как [math]p = 4[/math], то имеем [math]\frac{4!}{|\Gamma(P_{4})|} = 12[/math] и [math]\frac{4!}{|\Gamma(K_{1, 3})|} = 4[/math].

Теорема перечисления Пойа

Пойа показал, как получить формулу, перечисляющую орбиты в соответствии с весами и зависящую от циклической структуры подстановок данной группы.

Теорема:

Пусть [math]A[/math] — группа подстановок, действующая на множестве [math]X[/math] с орбитами [math]\Theta_{1}, \Theta_{2} \cdots \Theta_{n}[/math] и [math]\omega[/math] — функция, приписывающая веса каждой орбите (весовая функция). Более того, [math]\omega[/math] определяется на [math]X[/math] так, что [math]\omega(x) = \omega(\Theta_{i})[/math], если [math]x \in \Theta_{i}[/math]. Тогда сумма весов орбит равна [math]|A| \sum\limits_{i=1}^n \omega(\Theta_{i}) = \sum\limits_{\alpha \in A} \sum\limits_{x = \alpha x} \omega(x)[/math].

Доказательство:

[math]\triangleright[/math]

Уже упоминалось о том, что порядок [math]|A|[/math] группы [math]A[/math] равен [math]|A(x)| \cdot |\Theta(x)|[/math] для любого [math]x \in X[/math], где [math]A(x)[/math] — стабилизатор элемента [math]x[/math]. Так как весовая функция постоянна на элементах данной орбиты, то справедливо равенство [math]|\Theta_{i}| \omega(\Theta_{i}) = \sum\limits_{x \in \Theta_{i}}\omega(x)[/math] для каждой орбиты [math]\Theta_{i}[/math]. Домножив второе равенство на первое и сократив, получаем [math]|A| \omega(\Theta_{i}) = \sum\limits_{x \in \Theta_{i}}|A(x)|\omega(x)[/math]. Суммируя по всем орбитам, находим [math]|A|\sum\limits_{i=1}^n \omega(\Theta_{i}) = \sum\limits_{i=1}^n \sum\limits_{x \in \Theta_{i}}|A(x)|\omega(x)[/math], откуда непосредственно следует доказываемое соотношение.

[math]\triangleleft[/math]