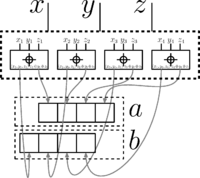Дерево Уоллеса — различия между версиями
Komarov (обсуждение | вклад) м |
Komarov (обсуждение | вклад) м (→Дерево Уоллеса) |
||
| Строка 8: | Строка 8: | ||
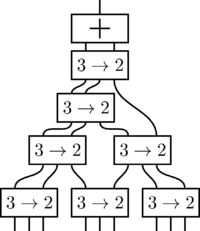
[[file:wallace_tree.png|thumb|200px|Иллюстрация работы дерева для суммирования 9 чисел]] | [[file:wallace_tree.png|thumb|200px|Иллюстрация работы дерева для суммирования 9 чисел]] | ||
| − | В отличие от ещё одной схемы для умножения | + | Для получения произведения, воспользуемся методом, напоминающим умножение «в столбик»: распишем произведение в сумму <tex>n</tex> |
| + | чисел (как в [[Матричный умножитель|матричном умножителе]]). | ||
| + | |||
| + | В отличие от ещё одной схемы для умножения — [[Матричный умножитель|матричного умножителя]], дерево Уоллеса складывает все числа не последовательно, а с помощью специального элемента(назовём его <tex>3\to2</tex>), преобразующего 3 числа <tex>x, y</tex> и <tex> z </tex> в числа <tex>a</tex> и <tex>b</tex> такие, что <tex>x + y + z = a + b</tex>. | ||
С помощью этого элемента на каждом шаге производятся следующие операции: | С помощью этого элемента на каждом шаге производятся следующие операции: | ||
Версия 04:21, 16 октября 2010
Содержание
Определение
Дерево Уоллеса - схема для умножения двух чисел.
Принцип работы
Дерево Уоллеса
Для получения произведения, воспользуемся методом, напоминающим умножение «в столбик»: распишем произведение в сумму чисел (как в матричном умножителе).
В отличие от ещё одной схемы для умножения — матричного умножителя, дерево Уоллеса складывает все числа не последовательно, а с помощью специального элемента(назовём его ), преобразующего 3 числа и в числа и такие, что .
С помощью этого элемента на каждом шаге производятся следующие операции:
- Берутся тройки чисел , , . При этом какие-то числа могут остаться.
- Для каждой тройки применяется элемент .
- Повторяются пункты 1 и 2 пока не осталось 2 числа.
- Оставшиеся 2 числа складываются с помощью двоичного каскадного сумматора.
На выходе имеем число, которое равно сумме чисел на всех входах.
Элемент 3→2
Теперь о том, как устроен элемент .
Для построения элемента нам потребуется элемент, который умеет складывать 3 бита и возвращать 2 бита результата. Основная идея реализации - отдельная обработка переносов и остатков.
Тогда первое число ответа может быть получена так: , где , и - входные числа, а , и - соответствующие их -е биты.
Второе же число можно получить так: , где - функция медианы (она же "голосование 2 из 3"). С помощью этой функции считается перенос.
Очевидно, полученные числа и дадут в сумме
Схемная сложность
Определим схемную сложность этого элемента.
Каждый элемент имеет глубину и размер .
Подсчитаем количество элементов . На каждом шаге количество чисел, которые нужно просуммировать, уменьшается в раза. Тогда глубина дерева будет равна , и в нём будет элементов . Тогда общая сложность равна
Литература
- Т. Кормен, Ч. Лейзерсон, Р. Ривест: Алгоритмы: построение и анализ, 1-е изд