Многомерное дерево отрезков — различия между версиями
(вместо + некоторая абстрактная операция, осмысленные имена переменных) |
(многомерный случай) |
||
| Строка 49: | Строка 49: | ||
t[vertexX][vertexY] = t[vertexX][vertexY * 2 + 1] <tex>\times</tex> t[vertexX][vertexY * 2 + 2] | t[vertexX][vertexY] = t[vertexX][vertexY * 2 + 1] <tex>\times</tex> t[vertexX][vertexY * 2 + 2] | ||
| − | Подсчет | + | Подсчет некоторой функции от элементов, лежащих в прямоугольной области: |
// first call - sumX(0, 0, n - 1, leftX, rightX, leftY, rightY, t) | // first call - sumX(0, 0, n - 1, leftX, rightX, leftY, rightY, t) | ||
| Строка 96: | Строка 96: | ||
t[vertexX][vertexY] = t[vertexX][vertexY * 2 + 1] <tex>\times</tex> t[vertexX][vertexY * 2 + 2] | t[vertexX][vertexY] = t[vertexX][vertexY * 2 + 1] <tex>\times</tex> t[vertexX][vertexY * 2 + 2] | ||
| + | ==Многомерный случай== | ||
| + | Рассмотрим, как изменяться функции при переходе к <tex>n</tex>-мерному случаю. | ||
| + | |||
| + | Например, для операции обновления дерева отрезков изменения будут следующими. В коде будут присутствовать <tex>n</tex> функций update (для каждой из координат). Реально будут только две различные реализации этих функций (первая, при нахождении необходимых листьев дерева, рекурсивно переходит к следующей координате, вторая {{---}} только возвращает значение из массива). Мы можем не писать <tex>n</tex> одинаковых реализаций в коде, но тогда дерево отрезков придется хранить не в <tex>n</tex>-мерном массиве, а в одномерном (это не сильно усложнит реализацию, но понятность кода уменьшится). | ||
| + | |||
| + | Рассмотрим более подробно устройство такой функции. В качестве параметров она должна принимать область, на которой считается операция, информацию о том, из каких ячеек массива мы рекурсивно спустились, отрезок, который обрабатывается по текущей координате и необходимый нам отрезок, а также номер текущей ячейки массива. | ||
| + | |||
| + | operationCalc(area[], x1, x2, ..., xP, leftBorder, rightBorder, needLeft, needRight, vertex) | ||
| + | |||
| + | Вначале следует проверить, что обрабатываемый отрезок не пустой (иначе вернуть нейтральный элемент для операции) | ||
| + | |||
| + | if leftBorder > rigthBorder | ||
| + | return 0 | ||
| + | |||
| + | Потом, если текущий отрезок совпадает с искомым, необходимо перейти к поиску по следующей координате | ||
| + | |||
| + | if leftBorder == needLeft && rightBorder == needRight | ||
| + | return operationCalc(area[], x1, x2, ..., xP, vertex, 0, m - 1, area[P + 2].left, area[P + 2].right, 0) | ||
| + | |||
| + | Если же отрезок не совпадает, то делим его пополам и рекурсивно вызываемся от его частей | ||
| + | |||
| + | med = (leftBorder + rightBorder) / 2 | ||
| + | return operationCalc(area[], x1, x2, ..., xP, leftBorder, med, needLeft, min(needRight, med), vertex * 2 + 1) <tex>\times</tex> | ||
| + | operationCalc(area[], x1, x2, ..., xP, med + 1, rightBorder, max(needLeft, med + 1), needRight, vertex * 2 + 2) | ||
| + | |||
| + | В реализации для последней координаты вместо рекурсивного перехода следует вернуть значение из массива | ||
| + | |||
| + | if leftBorder == needLeft && rightBorder == needRight | ||
| + | return t[x1][x2]...[xP][vertex] | ||
| + | |||
| + | Теперь рассмотрим операцию обновления. По аналогии напишем <tex>n</tex> функций, в каждой из которых сделаем следующее: | ||
| + | * Если рассматриваемый отрезок содержит больше одного элемента, разобьем его на две части и рекурсивно перейдем в ту, где находится необходимый элемент | ||
| + | * Перейдем к следующей координате или обновим массив (для последней координаты) | ||
| + | Псевдокод: | ||
| + | |||
| + | update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, rightBorder, vertex) | ||
| + | if leftBorder == rightBorder | ||
| + | if последняя координата | ||
| + | for I = 1..n | ||
| + | if xILeft != xIRigth | ||
| + | t[x1][x2]...[xP][vertex] = t[x1][x2]...[xI * 2 + 1]...[vertex] <tex>\times</tex> t[x1][x2]...[xI * 2 + 2]...[vertex] | ||
| + | return | ||
| + | t[x1][x2]...[xP][vertex] = newElem.value | ||
| + | else | ||
| + | update(newElem, x1, x2, ..., xP, vertex, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0) | ||
| + | else | ||
| + | med = (leftBorder + rightBorder) / 2 | ||
| + | if med >= newElem.x(P+1) | ||
| + | update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, med, vertex * 2 + 1) | ||
| + | else | ||
| + | update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, med + 1, vertex * 2 + 2) | ||
| + | update(newElem, x1, x2, ..., xP, vertex, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0) | ||
==Источники== | ==Источники== | ||
Версия 17:07, 25 мая 2012
Дерево отрезков естественным образом обобщается на двумерный и вообще говоря многомерный случай. Такая структура данных может вычислять значение некоторой ассоциативной функции на гиперпрямоугольнике за , где — размерность пространства, а — ширина гиперкуба на котором производятся вычисления.
Содержание
Структура
-мерное дерево отрезков — обычное дерево отрезков, элементами которого являются деревья отрезков размерности на 1 меньше. Основная идея заключается в рекурсивном переходе к деревьям меньшей размерности. Рассмотрим работу этого принципа на следующем примере. Пусть задано -мерное пространство с координатными осями . Необходимо вычислять некоторую ассоциативную функцию на гиперпрямоугольнике. Для этого сначала найдем элементы дерева, соответствующие координате. Для каждого из этих элементов рекурсивно перейдем в соответствующие им деревья отрезков и в них найдем элементы, отвечающие соответствующим координатам исходной гиперпрямоугольной области, и т. д. Таким образом, алгоритм совершит вхождений в рекурсию, каждая итерация которой работает за и получим необходимую асимптотику.
Двумерное дерево отрезков
Рассмотрим следующую задачу.
| Задача: |
Дано поле размером , заполненное некоторыми числами. Необходимо уметь обрабатывать два типа запросов:
|
Хранение
Двумерное дерево отрезков удобно хранить в виде массива, размером . Каждая строчка такого массива соответствует некоторому отрезку по первой координате. Сама же строчка является деревом отрезков по второй координате.
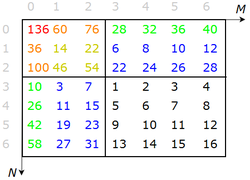
На рисунке справа показан пример дерева отрезков для суммы на массиве 4 на 4, заполненного числами от 1 от 16. Например, в элементе хранится сумма элементов, соответствующих отрезку по первой координате и по второй в исходном массиве. А в ячейке хранится сумма всех элементов.
Интересно, что если построить дерево вначале по второй координате, а потом по первой, то получившийся массив будет таким же. Т. е. данный двумерный массив можно рассматривать как массив деревьев отрезков, где каждое дерево соответствует некоторому отрезку по второй координате, а в нем хранятся суммы по первой.
Заметим, что в общем случае для хранения -мерного дерева отрезков требуется памяти, где — общее количество элементов.
Псевдокод для двумерного случая
Построение:
// first call - buildX(0, 0, n, a, t)
// a - исходный массив
// t - массив дерева отрезков
// [leftX, rightX) - полуинтервал
buildX(vertexX, leftX, rightX, a[][], t[][])
if leftX != rightX
mx = (leftX + rightX + 1) / 2
buildX(vertexX * 2 + 1, leftX, mx, a, t)
buildX(vertexX * 2 + 2, mx, rightX, a, t)
buildY(vertexX, leftX, rightX, 0, 0, m, a, t)
buildY(vertexX, leftX, rightX, vertexY, leftY, rightY, a[][], t[][])
if leftY == rightY
if leftX == rightX
t[vertexX][vertexY] = a[leftX][leftY]
else
t[vertexX][vertexY] = t[vertexX * 2 + 1][vertexY] t[vertexX * 2 + 2][vertexY]
else
my = (leftY + rightY + 1) / 2
buildY(vertexX, leftX, rightX, vertexY * 2 + 1, leftY, my, a, t)
buildY(vertexX, leftX, rightX, vertexY * 2 + 2, my, rightY, a, t)
t[vertexX][vertexY] = t[vertexX][vertexY * 2 + 1] t[vertexX][vertexY * 2 + 2]
Подсчет некоторой функции от элементов, лежащих в прямоугольной области:
// first call - sumX(0, 0, n - 1, leftX, rightX, leftY, rightY, t) sumX(vertexX, leftBorderX, rightBorderX, leftX, rightX, leftY, rightY, t[][]) if leftX > rightX return 0 if leftX == leftBorderX && rightX == rightBorderX return sumY(vertexX, 0, 0, m - 1, leftY, rightY) tmx = (leftBorderX + rightBorderX) / 2 return sumX(vertexX * 2 + 1, leftBorderX, tmx, leftX, min(rightX, tmx), leftY, rightY, t) sumX(vertexX * 2 + 2, tmx + 1, rightBorderX, max(leftX, tmx + 1), rightX, leftY, rightY, t) sumY(vertexX, vertexY, leftBorderY, rightBorderY, leftY, rightY) if leftY > rightY return 0 if leftY == leftBorderY && rightY == rightBorderY return t[vertexX][vertexY] tmy = (leftBorderY + rightBorderY) / 2 return sumY(vertexX, vertexY * 2 + 1, leftBorderY, tmy, leftY, min(rightY, tmy), t) sumY(vertexX, vertexY * 2 + 2, tmy + 1, rightBorderY, max(leftY, tmy + 1), rightY, t)
Обновление элемента:
// first call - updateX(0, 0, n - 1, x, y, val, t) updateX(vertexX, leftX, rightX, x, y, val, t[][]) if leftX != rightX mx = (leftX + rightX) / 2 if x <= mx updateX(vertexX * 2 + 1, leftX, mx, x, y, val, t) else updateX(vertexX * 2 + 2, mx + 1, rightX, x, y, val, t) updateY(vertexX, leftX, rightX, 0, 0, m - 1, x, y, val, t) updateY(vertexX, leftX, rightX, vertexY, leftY, rightY, x, y, val, t[][]) if leftY == rightY if leftX == rightX t[vertexX][vertexY] = val else t[vertexX][vertexY] = t[vertexX * 2 + 1][vertexY] t[vertexX * 2 + 2][vertexY] else my = (leftY + rightY) / 2 if y <= my updateY(vertexX, leftX, rightX, vertexY * 2 + 1, leftY, my, x, y, val, t) else updateY(vertexX, leftX, rightX, vertexY * 2 + 2, my + 1, rightY, x, y, val, t) t[vertexX][vertexY] = t[vertexX][vertexY * 2 + 1] t[vertexX][vertexY * 2 + 2]
Многомерный случай
Рассмотрим, как изменяться функции при переходе к -мерному случаю.
Например, для операции обновления дерева отрезков изменения будут следующими. В коде будут присутствовать функций update (для каждой из координат). Реально будут только две различные реализации этих функций (первая, при нахождении необходимых листьев дерева, рекурсивно переходит к следующей координате, вторая — только возвращает значение из массива). Мы можем не писать одинаковых реализаций в коде, но тогда дерево отрезков придется хранить не в -мерном массиве, а в одномерном (это не сильно усложнит реализацию, но понятность кода уменьшится).
Рассмотрим более подробно устройство такой функции. В качестве параметров она должна принимать область, на которой считается операция, информацию о том, из каких ячеек массива мы рекурсивно спустились, отрезок, который обрабатывается по текущей координате и необходимый нам отрезок, а также номер текущей ячейки массива.
operationCalc(area[], x1, x2, ..., xP, leftBorder, rightBorder, needLeft, needRight, vertex)
Вначале следует проверить, что обрабатываемый отрезок не пустой (иначе вернуть нейтральный элемент для операции)
if leftBorder > rigthBorder return 0
Потом, если текущий отрезок совпадает с искомым, необходимо перейти к поиску по следующей координате
if leftBorder == needLeft && rightBorder == needRight return operationCalc(area[], x1, x2, ..., xP, vertex, 0, m - 1, area[P + 2].left, area[P + 2].right, 0)
Если же отрезок не совпадает, то делим его пополам и рекурсивно вызываемся от его частей
med = (leftBorder + rightBorder) / 2
return operationCalc(area[], x1, x2, ..., xP, leftBorder, med, needLeft, min(needRight, med), vertex * 2 + 1)
operationCalc(area[], x1, x2, ..., xP, med + 1, rightBorder, max(needLeft, med + 1), needRight, vertex * 2 + 2)
В реализации для последней координаты вместо рекурсивного перехода следует вернуть значение из массива
if leftBorder == needLeft && rightBorder == needRight return t[x1][x2]...[xP][vertex]
Теперь рассмотрим операцию обновления. По аналогии напишем функций, в каждой из которых сделаем следующее:
- Если рассматриваемый отрезок содержит больше одного элемента, разобьем его на две части и рекурсивно перейдем в ту, где находится необходимый элемент
- Перейдем к следующей координате или обновим массив (для последней координаты)
Псевдокод:
update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, rightBorder, vertex)
if leftBorder == rightBorder
if последняя координата
for I = 1..n
if xILeft != xIRigth
t[x1][x2]...[xP][vertex] = t[x1][x2]...[xI * 2 + 1]...[vertex] t[x1][x2]...[xI * 2 + 2]...[vertex]
return
t[x1][x2]...[xP][vertex] = newElem.value
else
update(newElem, x1, x2, ..., xP, vertex, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0)
else
med = (leftBorder + rightBorder) / 2
if med >= newElem.x(P+1)
update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, med, vertex * 2 + 1)
else
update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, med + 1, vertex * 2 + 2)
update(newElem, x1, x2, ..., xP, vertex, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0)