Fusion tree — различия между версиями
Kamensky (обсуждение | вклад) м (s[A-z]etch -> sketch; Succ -> succ) |
Kamensky (обсуждение | вклад) м (Тире заменено шаблоном) |
||
| Строка 8: | Строка 8: | ||
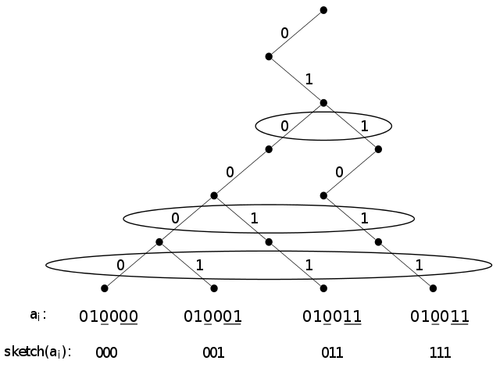
[[Файл:Fusion.png||500x400px|center|визуализация функции sketch]] | [[Файл:Fusion.png||500x400px|center|визуализация функции sketch]] | ||
| − | В Fusion tree вместе с ключом <tex>x</tex> хранится <tex>sketch(x)</tex> - последовательность битов <tex>x_{b_{r-1}}\ldots x_{b_0}</tex>. | + | В Fusion tree вместе с ключом <tex>x</tex> хранится <tex>sketch(x)</tex> {{---}} последовательность битов <tex>x_{b_{r-1}}\ldots x_{b_0}</tex>. |
{{Утверждение | {{Утверждение | ||
|id=sketch. | |id=sketch. | ||
| Строка 20: | Строка 20: | ||
==Поиск вершины== | ==Поиск вершины== | ||
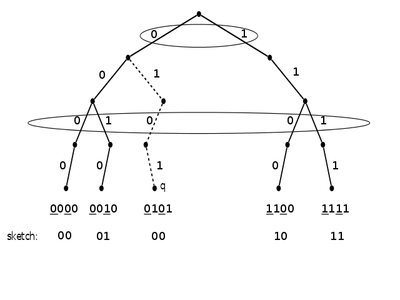
[[Файл:FusionTree.png|400x400px|thumb|right|пример случая, когда <tex>sketch(a_i) \leqslant sketch(q) \leqslant sketch(a_{i+1})</tex>, но <tex>a_{i+1}\leqslant q</tex>]] | [[Файл:FusionTree.png|400x400px|thumb|right|пример случая, когда <tex>sketch(a_i) \leqslant sketch(q) \leqslant sketch(a_{i+1})</tex>, но <tex>a_{i+1}\leqslant q</tex>]] | ||
| − | Пусть <tex>\left \{ a_1,a_2\ldots a_k\right \}</tex> - множество ключей узла, отсортированных по возрастанию, <tex>q</tex> - ключ искомой вершины, <tex>l</tex> - количество бит в <tex>sketch(q)</tex>. Сначала найдем такой ключ <tex>a_i</tex>, что <tex>sketch(a_i) \leqslant sketch(q) \leqslant sketch(a_{i+1})</tex>. Но положение <tex>sketch(q)</tex> среди <tex>sketch(a_j)</tex> не всегда эквивалентно положению <tex>q</tex> среди <tex>a_j</tex>, поэтому, зная соседние элементы <tex>sketch(q)</tex>, найдем <tex>succ(q)</tex> и <tex>pred(q)</tex>. | + | Пусть <tex>\left \{ a_1,a_2\ldots a_k\right \}</tex> {{---}} множество ключей узла, отсортированных по возрастанию, <tex>q</tex> {{---}} ключ искомой вершины, <tex>l</tex> {{---}} количество бит в <tex>sketch(q)</tex>. Сначала найдем такой ключ <tex>a_i</tex>, что <tex>sketch(a_i) \leqslant sketch(q) \leqslant sketch(a_{i+1})</tex>. Но положение <tex>sketch(q)</tex> среди <tex>sketch(a_j)</tex> не всегда эквивалентно положению <tex>q</tex> среди <tex>a_j</tex>, поэтому, зная соседние элементы <tex>sketch(q)</tex>, найдем <tex>succ(q)</tex> и <tex>pred(q)</tex>. |
===Параллельное сравнение=== | ===Параллельное сравнение=== | ||
Найдем <tex>succ(sketch(q))</tex> и <tex>pred(sketch(q))</tex>. Определим <tex>sketch(node)</tex> как число, составленное из единиц и <tex>sketch(a_i)</tex>, то есть <tex>sketch(node) = 1sketch(a_1)1sketch(a_2)\ldots 1sketch(a_k)</tex>. Вычтем из <tex>sketch(node)</tex> число <tex>sketch(q) \times \underbrace{\overbrace{00\ldots 1}^{l + 1 bits}\overbrace{00\ldots 1}^{l + 1 bits}\ldots \overbrace{00\ldots 1}^{l + 1 bits}}_{k(l + 1) bits} = 0sketch(q)\ldots 0sketch(q)</tex>. В начале каждого блока, где <tex>sketch(a_i) \geqslant sketch(q)</tex>, сохранятся единицы. Применим к получившемуся побитовое ''AND'' c <tex>\displaystyle \sum_{i=0}^{k-1}2^{i(l+1)+l}</tex>, чтобы убрать лишние биты. | Найдем <tex>succ(sketch(q))</tex> и <tex>pred(sketch(q))</tex>. Определим <tex>sketch(node)</tex> как число, составленное из единиц и <tex>sketch(a_i)</tex>, то есть <tex>sketch(node) = 1sketch(a_1)1sketch(a_2)\ldots 1sketch(a_k)</tex>. Вычтем из <tex>sketch(node)</tex> число <tex>sketch(q) \times \underbrace{\overbrace{00\ldots 1}^{l + 1 bits}\overbrace{00\ldots 1}^{l + 1 bits}\ldots \overbrace{00\ldots 1}^{l + 1 bits}}_{k(l + 1) bits} = 0sketch(q)\ldots 0sketch(q)</tex>. В начале каждого блока, где <tex>sketch(a_i) \geqslant sketch(q)</tex>, сохранятся единицы. Применим к получившемуся побитовое ''AND'' c <tex>\displaystyle \sum_{i=0}^{k-1}2^{i(l+1)+l}</tex>, чтобы убрать лишние биты. | ||
| Строка 41: | Строка 41: | ||
Сравнивая <tex>a \oplus q</tex> и <tex>b \oplus q</tex>, найдем какой из ключей имеет наибольший общий префикс с <tex>q</tex> (наименьшее значение соответствует наибольшей длине). | Сравнивая <tex>a \oplus q</tex> и <tex>b \oplus q</tex>, найдем какой из ключей имеет наибольший общий префикс с <tex>q</tex> (наименьшее значение соответствует наибольшей длине). | ||
| − | Предположим, что <tex>p</tex> - наибольший общий префикс, а <tex>y</tex> его длина, <tex>a_j</tex> - ключ, имеющий наибольший общий префикс с <tex>q</tex> (<tex>j = i</tex> или <tex>i+1</tex>). | + | Предположим, что <tex>p</tex> {{---}} наибольший общий префикс, а <tex>y</tex> его длина, <tex>a_j</tex> {{---}} ключ, имеющий наибольший общий префикс с <tex>q</tex> (<tex>j = i</tex> или <tex>i+1</tex>). |
* если <tex>q>a_j</tex>, то <tex>y + 1</tex> бит <tex>q</tex> равен единице, а <tex>y + 1</tex> бит <tex>a_j</tex> равен нулю. Так как общий префикс <tex>a_j</tex> и <tex>q</tex> является наибольшим, то не существует ключа с префиксом <tex>p1</tex>. Значит, <tex>q</tex> больше всех ключей с префиксом меньшим либо равным <tex>p</tex>. Найдем <tex>pred(e)</tex>, <tex>e = p01\ldots 11</tex>, который одновременно будет <tex>равен pred(q)</tex>; | * если <tex>q>a_j</tex>, то <tex>y + 1</tex> бит <tex>q</tex> равен единице, а <tex>y + 1</tex> бит <tex>a_j</tex> равен нулю. Так как общий префикс <tex>a_j</tex> и <tex>q</tex> является наибольшим, то не существует ключа с префиксом <tex>p1</tex>. Значит, <tex>q</tex> больше всех ключей с префиксом меньшим либо равным <tex>p</tex>. Найдем <tex>pred(e)</tex>, <tex>e = p01\ldots 11</tex>, который одновременно будет <tex>равен pred(q)</tex>; | ||
| − | * если <tex>q<a_j</tex> - найдем <tex>succ(e)</tex>, <tex>e = p10\ldots 00</tex>. Это будет <tex>succ(q)</tex>. | + | * если <tex>q<a_j</tex> {{---}} найдем <tex>succ(e)</tex>, <tex>e = p10\ldots 00</tex>. Это будет <tex>succ(q)</tex>. |
Длина наибольшего общего префикса двух ''w''-битных чисел <tex>a</tex> и <tex>b</tex> может быть вычислена с помощью нахождения индекса наиболее значащего бита в побитовом ''XOR'' <tex>a</tex> и <tex>b</tex>. | Длина наибольшего общего префикса двух ''w''-битных чисел <tex>a</tex> и <tex>b</tex> может быть вычислена с помощью нахождения индекса наиболее значащего бита в побитовом ''XOR'' <tex>a</tex> и <tex>b</tex>. | ||
Версия 04:31, 16 июня 2014
Fusion tree — дерево поиска, позволяющее хранить -битных чисел, используя памяти, и выполнять операции поиска за время . Эта структура данных была впервые предложена в 1990 году М. Фредманом (M. Fredman) и Д. Уиллардом (D. Willard).
Содержание
Структура
Fusion tree — это B-дерево, такое что:
- у всех вершин, кроме листьев, детей;
- время, за которое определяется, в каком поддереве находится вершина, равно .
Такое время работы достигается за счет хранения дополнительной информации в вершинах. Построим цифровой бор из ключей узла дерева. Всего ветвящихся вершин. Биты, соответствующие уровням дерева, в которых происходит ветвление, назовем существенными и обозначим их номера . Количество существенных битов не больше чем .
В Fusion tree вместе с ключом хранится — последовательность битов .
| Утверждение: |
сохраняет порядок, то есть , если . |
| Рассмотрим наибольший общий префикс и . Тогда следующий бит определяет их порядок и одновременно является существенным битом. Поэтому, если , то и . |
Поиск вершины
Пусть — множество ключей узла, отсортированных по возрастанию, — ключ искомой вершины, — количество бит в . Сначала найдем такой ключ , что . Но положение среди не всегда эквивалентно положению среди , поэтому, зная соседние элементы , найдем и .
Параллельное сравнение
Найдем и . Определим как число, составленное из единиц и , то есть . Вычтем из число . В начале каждого блока, где , сохранятся единицы. Применим к получившемуся побитовое AND c , чтобы убрать лишние биты.
AND
Если , то , в противном случае . Теперь надо найти количество единиц в L. Умножим L на , тогда все единицы сложатся в первом блоке результата, и, чтобы получить количество единиц, сдвинем его вправо.
succ(q) и pred(q)
Пусть .
| Утверждение: |
Среди всех ключей наибольший общий префикс с будет иметь или или . |
| Предположим, что имеет наибольший общий префикс с . Тогда будет иметь больше общих битов со . Значит, ближе по значению к , чем или , что приводит к противоречию. |
Сравнивая и , найдем какой из ключей имеет наибольший общий префикс с (наименьшее значение соответствует наибольшей длине).
Предположим, что — наибольший общий префикс, а его длина, — ключ, имеющий наибольший общий префикс с ( или ).
- если , то бит равен единице, а бит равен нулю. Так как общий префикс и является наибольшим, то не существует ключа с префиксом . Значит, больше всех ключей с префиксом меньшим либо равным . Найдем , , который одновременно будет ;
- если — найдем , . Это будет .
Длина наибольшего общего префикса двух w-битных чисел и может быть вычислена с помощью нахождения индекса наиболее значащего бита в побитовом XOR и .
Вычисление sketch(x)
Чтобы найти sketch за константное время, будем вычислять , имеющий все существенные биты в нужном порядке, но содержащий лишние нули.
1) уберем все несущественные биты AND ;
2) умножением на некоторое заранее вычисленное число сместим все существенные биты в блок меньшего размера.
;
3) применив побитовое AND, уберем лишние биты, появившиеся в результате умножения;
AND ;
4) сделаем сдвиг вправо на бит.
| Утверждение: |
Дана последовательность из чисел . Тогда существует последовательность , такая что:
1) все различны, для ; 2) ; 3) . |
|
Выберем некоторые , таким образом, чтобы . Предположим, что мы выбрали . Тогда . Всего недопустимых значений для , поэтому всегда можно найти хотя бы одно значение. Чтобы получить , выбираем каждый раз наименьшее и прибавляем подходящее число кратное , такое что . |
Первые два условия необходимы для того, чтобы сохранить все существенные биты в нужном порядке. Третье условие позволит поместить sketch узла в w-битный тип. Так как , то будет занимать бит.
Индекс наиболее значащего бита
Чтобы найти в w-битном числе индекс самого старшего бита, содержащего единицу, разделим на блоков по бит. . Далее найдем первый непустой блок и индекс первого единичного бита в нем.
1) Поиск непустых блоков.
a. Определим, какие блоки имеют единицу в первом бите. Применим побитовое AND к и константе .
b. Определим, содержат ли остальные биты единицы.
Вычислим .
Вычтем из . Если какой-нибудь бит обнулится, значит, соответствующий блок содержит единицы.
Чтобы найти блоки, содержащие единицы, вычислим .
c. Первый бит в каждом блоке OR содержит единицу, если соответствующий блок ненулевой.
2) Найдем , чтобы сместить все нужные биты в один блок. Существенными битами в данном случае будут первые биты каждого блока, поэтому .
Будем использовать . Тогда . Все суммы различны при . Все возрастают, и .
Чтобы найти , умножим на и сдвинем вправо на бит.
3) Найдем первый ненулевой блок. Для этого надо найти первую единицу в . Как и при поиске и используем параллельное сравнение с . В результате сравнения получим номер первого ненулевого блока .
4) Найдем номер первого единичного бита в найденном блоке так же как и в предыдущем пункте.
5) Индекс наиболее значащего бита будет равен .
Каждый шаг выполняется за , поэтому всего потребуется времени, чтобы найти индекс.
Ссылки
MIT CS 6.897: Advanced Data Structures: Lecture 4, Fusion Trees, Prof. Erik Demaine (Spring 2003)