Задача многокритериальной оптимизации. Multiobjectivization

Задача многокритериальной оптимизации

Постановка задачи

Определение:

Задача многокритериальной оптимизации: [math]maximize \{f(x) = (f_1(x),\dots,f_K(x))\}[/math] [math] x \in X[/math] где [math] f(x) : X \rightarrow R^K[/math] - целевая вектор-функция, где [math]K \ge 2[/math]

Так как не существует единого решение, которое было бы максимальным для всех целевых функций, вместо него можно искать множество [math]X^* \subseteq X [/math] множество Парето оптимальных значений.

Множество Парето оптимальных значений

Определение:

Множество Парето оптимальных значений: [math]\forall x^* \in X^* \not\exists x \in X [/math]:[math]x \succ x^*[/math], где [math]x \succ x^* \Leftrightarrow (\forall i \in 1..K, (f_i(x) \ge f_i(x^*))\land (\exists i \in 1..K, f_i(x) \gt f_i(x^*)))[/math]

Выражение [math]x \succ x^*[/math] означает, что [math]x[/math] доминирует над [math]x^*[/math].

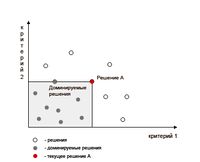
Говорят, что [math]x[/math] доминирует над [math]x^*[/math]. по Парето, если [math]x[/math] не хуже [math]x^*[/math] по всем критериям и хотя бы по одному критерию превосходит [math]x^*[/math]. В таком случае в выборе [math]x^*[/math] нет смысла, т.к. [math]x[/math] по всем параметрам не уступает, а по каким-то и превосхожит [math]x^*[/math]. Если рассматривать всего два критерия то на рис. 1 показана область пространства, доминируемая данным решением А. Эта область «замкнута»: элементы на ее границе также доминируемы А

Рис.1 - Доминируемые решения

Определение:

Для двух решений [math]x[/math] и [math]x'[/math] говорят [math]x \sim x'[/math] тогда и только тогда, когда [math]\exists i \in 1..K \colon f_i(x) \gt f_i(x') \land \exists j \in 1..K, j \ne i \colon f_j(x') \gt f_j(x)[/math] - такую пару решений называют недоминируемой

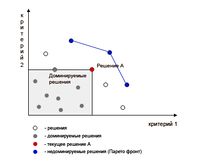
На рис. 2 показана граница Парето для возможных решений в двухкритериальном пространстве

Рис.2 - Парето фронт

Множество Парето оптимальных недоминируемых решений называется Парето фронтом.

Multi-objectivization

Суть метода мульти-объективизации заключается в разбитии сложной задачи с одной целевой функцией на несколько подзадач, найти для каждой подзадачи решение и выбрать оптимальное решение.

Для выполнения оптимизации многокритериальной задачи мы должны добавить в целевую функцию новые параметры, либо должны добавить новые целевые функции.

Сложность этой процедуры заключается в разложении проблемы на ряд мелких независимых между собой подпроблем.

Алгоритмы

Hill-Climbers

Initialization:	[math]P \leftarrow \emptyset [/math] Init_pop[math](P)[/math]
Main Loop:	[math]x_1 \leftarrow [/math]Rand_mem[math](P)[/math],[math]x'_2 \leftarrow [/math]Rand_mem[math](P)[/math] [math]x'_1 \leftarrow [/math]Mutate[math](P)[/math],[math]x_2 \leftarrow [/math]Mutate[math](P)[/math] if[math](H(x_1,x'_1)+H(x_2,x'_2) \gt H(x_1,x'_2)+H(x_2,x'_1))[/math] Swap[math](x_1,x'_2)[/math] if [math]f(x'_1) \gt f(x_1)[/math] [math]P \leftarrow P \cup x'_1 \setminus x_1[/math] if [math]f(x'_2) \gt f(x_2)[/math] [math]P \leftarrow P \cup x'_2 \setminus x_2[/math]
Termination:	return Best[math](P)[/math]

Источники

• Википедия: Многокритериальная оптимизация
• Knowles J., Watson R., Corne D. Reducing Local Optima in Single-Objective Problems by Multi-objectivization
• Friedrich T., Neumann F. Foundations of Evolutionary Multi-Objective Optimization