Генерация комбинаторных объектов в лексикографическом порядке

Определение

Генерация комбинаторных объектов в лексикографическом порядке — непосредственное построение и перебор всех объектов заданного типа так, чтобы для любых двух объектов выполнялось условие: [math]K_i[/math] [math]\lt [/math] [math]K_i[/math][math]_+[/math][math]_1[/math].

Алгоритм построения

Описание процедуры построения

Пусть [math]Gen(p, K)[/math] - процедура генерирования, где [math]p[/math] - глубина рекурсии, [math]K[/math] - комбинаторный объект.

Gen(p, K)
  if p = <требуемый размер объекта>
    <выводим> K
  else
     for <все w из алфавита на котором строится K>
       if (K + w) = <корректный префикс требуемого объекта>
         Gen(p + 1, K + w)

Генерация с помощью процедуры получения следующего объекта

Составляем первый объект - [math]K_1[/math], для него получаем следующий объект - [math]K_2[/math], для [math]K_2[/math] получаем [math]K_3[/math], далее действуем также, для [math]K_i[/math] получая [math]K_i[/math][math]_+[/math][math]_1[/math] объект, пока не получим последний объект [math]K_n[/math].

Примеры

Пример генерации сочетаний из N элементов по K в лексикографическом порядке

Первым сочетанием, очевидно, будет сочетание [math](1,2,...,K)[/math]. Научимся для текущего сочетания находить лексикографически следующее. Для этого в текущем сочетании найдём самый правый элемент, не достигший ещё своего наибольшего значения; тогда увеличим его на единицу, а всем последующим элементам присвоим наименьшие значения.

Пусть [math]next_combination (a, n)[/math] - процедура генерирования, где [math]a[/math] - текущее сочетание, [math]n[/math] - количество элементов.

bool next_combination (vector<int> & a, int n) {
int k = (int)a.size();
  for (int i=k-1; i>=0; --i)
          if (a[i] < n-k+i+1) {
                  ++a[i];
                  for (int j=i+1; j<k; ++j)
                          a[j] = a[j-1]+1;
                  return true;
          }
  return false;
}

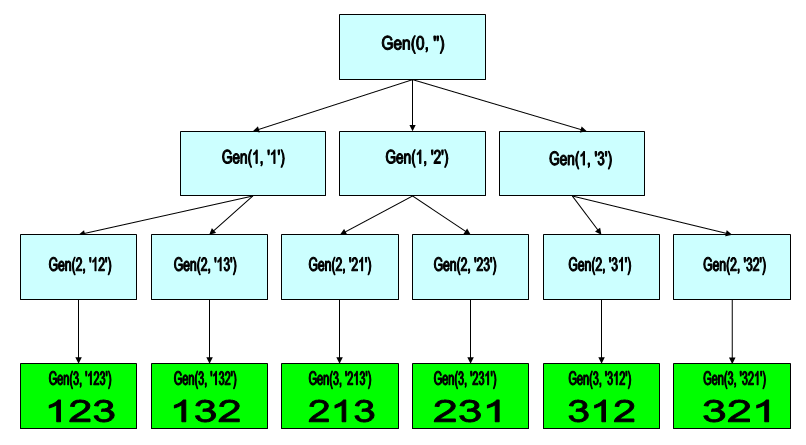
Пример работы процедуры генерации

Иллюстрация работы процедуры генерирования всех перестановок из чисел [math]1, 2, 3[/math]

Ссылки

• Перечисление (комбинаторика)
• ДИСКРЕТНАЯ МАТЕМАТИКА: АЛГОРИТМЫ
• Комбинаторика и переборные задачи
• Комбинаторика