Базовые определения и формализм — различия между версиями
Anverk (обсуждение | вклад) (→Условия согласованности) |
м (rollbackEdits.php mass rollback) |
| (не показана 1 промежуточная версия 1 участника) | |
(нет различий)
| |
Текущая версия на 19:34, 4 сентября 2022
Содержание
Определения
Базовые определения
| Определение: |
|
Исполнение системы это пара , где:
Замечание: чаще всего исполнение понятно из контекста и опускается Обозначение: |
| Определение: |
| Система это множество всех возможных исполнений. Говорим, что система имеет свойство , если каждое исполнение системы имеет свойство |
| Определение: |
|
Модель глобального времени определим так, что это модель, в которой в качестве операции используется временной интервал: причём . Зададим в этой модели отношение следующим образом: . Неформально это означает, что вход в функцию, выполняющую операцию , был осуществлён строго позже, чем был получен результат работы функции, выполняющей операцию . Замечание: глобального времени не существует из-за физических ограничений, поэтому в доказательствах такая модель не используется, но помогает при визуализации различных исполнений |
| Определение: |
| Исполнение системы называется последовательным, если . То есть, если все операции линейно-упорядочены отношением "произошло до". |
Конфликты и гонки данных
| Определение: |
| Две операции над одной переменной, одна из которых это запись, называются конфликтующими. Соответственно, бывают read-write и write-write конфликты. |
| Определение: |
| Если две конфликтующие операции произошли параллельно, то такая ситуация называется гонка данных (англ. data race) Замечание: наличие гонки данных является свойством конкретного исполнения. |
| Определение: |
| Программа называется корректно синхронизированной, если в любом допустимом исполнении нет гонок данных. |
Правильное исполнение
| Определение: |
|
Сужение исполнения на поток исполнение, в котором остались только операции, происходящие в потоке . |
| Определение: |
| Объединение всех сужений на потоки называется программным порядком (англ. program order или po). |
| Определение: |
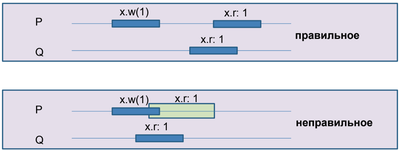
| Сужение исполнения на объект исполнение, в котором остались только операции, взаимодействующие с объектом . Обозначение: . Формально Замечание: в правильном исполнении сужение на объекты не всегда является последовательным |
Условия согласованности
| Определение: |
| Согласованность является аналогом корректности в многопоточном программировании. Базовое требование согласованности: корректные последовательные программы должны cчитаться согласованными при любом их исполнении в одном потоке |
| Определение: |
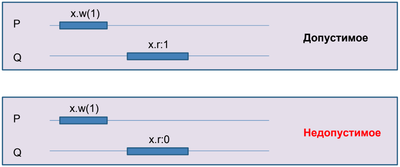
| Последовательное исполнение является допустимым (англ. legal), если выполнены последовательные спецификации всех объектов. |
| Определение: |
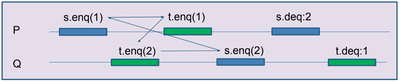
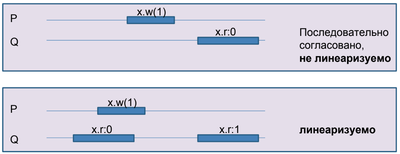
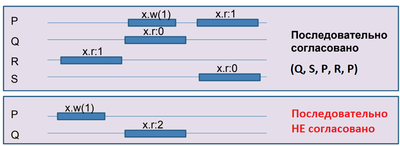
| Исполнение последовательно согласовано, если можно сопоставить эквивалентное ему (состоящее из тех же событий и операций) допустимое последовательное исполнение, которое сохраняет программный порядок, то есть порядок операций на каждом потоке. Замечание: Последовательная согласованность на каждом объекте не влечёт последовательную согласованность исполнения |
| Определение: |
| Исполнение линеаризуемо, если существует эквивалентное ему допустимое последовательное исполнение , называемое линеаризацией, и верно что , то есть сохраняется отношение "произошло до". |
Декомпозиция исполнения
| Определение: |
Определим декомпозицию исполнения как пятёрку , где
|
| Определение: |
| Определим произошло до на операциях: |
Свойства линеаризуемости
| Определение: |
Пусть дана декомпозиция . Тогда определим точки линеаризации как функцию такую, что:
|
| Утверждение (эквивалентное определение линеаризуемости): |
Пусть дана декомпозиция .
Исполнение является линеаризуемым тогда и только тогда, когда верны два условия:
|
|
Пусть есть точки линеаризации , полный порядок над ними. Требуется найти линеаризацию . Определим как , так как они по определению линеаризации должны быть эквивалентны, а определим, воспользовавшись вторым условием предпосылки. Докажем корректность такой линеаризации, то есть что :
Добавим события в такие, что и для которых выполнено требование из . Эти точки и будут точками линеаризации. Итак, построены точки линеаризации, которые, очевидно, сохраняют линеаризацию по их построению. |
Следствие 1. Для модели глобального времени эта теорема верна в обе стороны: действительно дополнительное требование выполняется, так как каждая операция в нём является непрерывным множеством.
Следствие 2. Чтобы среди точек линеаризации был порядок, согласованный с семантикой низкоуровневых операций, достаточно чтобы операции низкого уровня были атомарны (линеаризуемы)
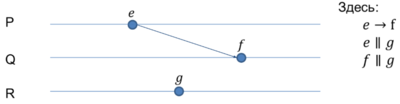
![Отношения между операциями [math] e, f, g [/math] процессов [math] P, Q, R [/math] в модели глобального времени](/wiki/images/thumb/2/2c/Global_time_modeling.png/400px-Global_time_modeling.png)