Алгоритм Эдмондса-Карпа

Алгоритм

Алгоритм Эдмондса-Карпа является реализацией метода Форда-Фалкерсона, в которой в качестве дополняющего пути выбирается кратчайший по рёбрам путь в остаточной сети (длины всех рёбер равны $1$).

Описание

1. Положим все потоки равными нулю. Остаточная сеть изначально совпадает с исходной сетью.
2. В остаточной сети находим кратчайший путь из источника в сток. Если такого пути нет, останавливаемся.
3. Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток:
   1. На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью $\mathrm{c_{min}}$.
   2. Для каждого ребра на найденном пути увеличиваем поток на $\mathrm{c_{min}}$, а в противоположном ему — уменьшаем на $\mathrm{c_{min}}$.
   3. Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его.
4. Возвращаемся на шаг 2.

Сложность

Сложность алгоритма Эдмондса-Карпа равна $O(VE^2)$.

Псевдокод

function EdmondsKarp(G, s, t):
    for (для) каждого ребра $(u,v) \in E[G]$
        $f[u,v] \leftarrow 0$
        $f[v,u] \leftarrow 0$
    while существует кратчайший путь $p$ из $s$ в $t$ в остаточной сети $G_f$
        $c_f(p) \leftarrow min\{c_f(u,v) : (u,v) \in p\}$
        for $(u,v) \in p$
            $f[u,v] \leftarrow f[u,v] + c_f(p)$
            $f[v,u] \leftarrow -f[u,v]$

Корректность алгоритма Эдмондса-Карпа

На каждой итерации цикла $\mathrm {while}$ поток в графе $G$ увеличивается вдоль одного из кратчайших путей в $G_f$ из истока $s$ в сток $t$. Этот процесс повторяется до тех пор пока существует кратчайший $s \leadsto t$ путь в $G_f$. Если в $G_f$ не существует кратчайшего пути из $s$ в $t$, значит, не существует вообще никакого $s \leadsto t$ пути в $G_f$ следовательно по теореме Форда-Фалкерсона найденный поток $f$ максимальный.

Оценка быстродействия

Лемма:

Если в сети $G(V,E)$ с истоком $s$ и стоком $t$ увеличение потока производится вдоль кратчайших $s \leadsto t$ путей в $G_f$, то для всех вершин $v \in V\backslash\{s,t\}$ длина кратчайшего пути $\delta_f(s, v)$ в остаточной сети $G_f$ не убывает после каждого увеличения потока.

Доказательство:

$\triangleright$

Предположим противное, пусть существует вершина $v \in V \backslash\{s,t\}$, что после какого-то увеличения потока длина кратчайшего пути из $s$ в $v$ уменьшилась. Обозначим потоки до и после увеличения соответственно за $f$ и $f'$. Пусть $v$ — вершина, расстояние $\delta'_f(s,v)$ от $s$ до которой минимально и уменьшилось с увеличением потока. Имеем $\delta'_f(s,v) \lt \delta_f(s,v)$. Рассмотрим путь $p = s \leadsto u \rightarrow v$, являющийся кратчайшим от $s$ к $v$ в $G'_f$. Тогда верно, что $\delta'_f(s, u) = \delta'_f(s,v) - 1$. По выбору $v$ и из предыдущего утверждения получаем, что $\delta'_f (s, u) \geqslant\delta_f(s,u)$. Предположим $(u, v) \in E_f$, тогда $\delta_f(s,v) \leqslant \delta_f(s, u) + 1 \leqslant \delta'_f(s,u) + 1 = \delta'_f(s, v)$. Это противоречит $\delta'_f(s,v) \lt \delta_f(s,v)$. Пусть $(u,v) \notin E_f$, но известно, что $(u,v) \in E_f'$. Появление ребра $(u,v)$ после увеличения потока означает увеличение потока по обратному ребру $(v, u)$. Увеличение потока производится вдоль кратчайшего пути, поэтому кратчайший путь из $s$ в $u$ вдоль которого происходило увеличения выглядит как $s \leadsto v \rightarrow u$, из чего получаем $\delta_f(s, v) = \delta_f(s, u) - 1 \leqslant \delta'_f(s, u) - 1 = \delta'(s, v) - 2$. Данное утверждение противоречит $\delta'_f(s,v) \lt \delta_f(s,v)$. Итак мы пришли к противоречию с существованием вершины $v$, кратчайшее расстояние до которой уменьшилось с увеличением потока.

$\triangleleft$

Опираясь на предшествующую лемму, докажем следующую теорему, которая ограничивает сверху число итераций цикла $\mathrm {while}$ в алгоритме Эдмондса-Карпа.

Теорема:

Пусть для некоторой сети $G(V,E)$ с источником $s$ и стоком $t$ выполняется алгоритм Эдмондса-Карпа, тогда общее число итераций цикла $\mathrm {while}$ составляет $O(V E)$.

Доказательство:

$\triangleright$

Рассмотрим множество рёбер $(u,v)$ остаточной сети $G_f$, принадлежащих увеличивающему пути $p$, таких что $c_f(p) = c_f(u,v)$. Назовем данные рёбра критическими. Покажем, что каждое из $|E|$ рёбер может становиться критическим не более, чем $|V| - 1$ раз. Заметим, что после увеличения потока вдоль пути $p$ все критические рёбра исчезают из остаточной сети, кроме того по определению остаточной пропускной способности пути хотя бы одно ребро увеличивающего пути — критическое. Рассмотрим две вершины $u$ и $v$ принадлежащие $V$, соединенные некоторым ребром из $E$. Увеличение производится вдоль кратчайших путей, поэтому если ребро $(u,v)$ становиться критическим в первый раз, верно, что $\delta_f(s,v) = \delta_f(s,u) + 1$. После увеличения потока ребро $(u, v)$ исчезает из сети. Оно не появится в другом увеличивающем пути до тех, пор пока не будет уменьшено по обратному ребру $(v, u)$. Это может произойти только в том случае, если ребро $(v, u)$ встретится на некотором увеличивающем пути. Пусть в момент перед увеличением поток в сети $G$ составлял $f'$, то поскольку увеличение производиться вдоль кратчайших путей, верно: $\delta'_f(s,u) = \delta'_f(s, v) + 1$. Согласно лемме $\delta_f(s,v) \leqslant \delta'_f(s,v)$, откуда $\delta'_f(s,u) = \delta'(s,v) + 1 \geqslant \delta_f(s,v) + 1 = \delta_f(s,u) + 2$. Итак в промежуток времени между тем, когда ребро $(u,v)$ становится критическим в первый раз, до момента, когда оно становится критическим в следующий раз, расстояние от $s$ до $u$ увеличивается минимум на $2$. Расстояние $\delta(s,u)$ в начальный момент времени больше либо равно $0$. Среди промежуточных вершин на кратчайшем пути $s \leadsto u$ не могут находиться $s$, $u$ или $t$. Следовательно к тому моменту, когда вершина $u$ станет недостижимой из источника расстояние до нее не превысит $|V| - 2$. Получаем, что ребро $(u, v)$ могло стать критическим не более $\dfrac{(|V| -2)}{2} = \dfrac{|V|}{2} - 1$ раз. Поскольку в графе не более $O(E)$ пар вершин, между которыми могут существовать рёбра в остаточной сети, то общее количество критических рёбер в ходе выполнения алгоритма Эдмондса-Карпа равно $O(V E)$. Так как каждый увеличивающий путь содержит по крайней мере одно критическое ребро, следовательно число кратчайших путей составляет $O(V E)$. На каждой итерации цикла $\mathrm {while}$ рассматривается ровно один увеличивающий путь, а поскольку в случае отсутствия такого пути выполнение цикла прерывается, то число итераций цикла $\mathrm {while}$ также составляет $O(V E)$.

$\triangleleft$

Если увеличивающий путь находить поиском в ширину, то каждую итерацию цикла $\mathrm {while}$ можно выполнить за время $O(E)$. Инициализация в процедуре Edmonds Karp производится за $O(E)$, следовательно время работы алгоритма алгоритма Эдмондса-Карпа составляет $O(V E^2)$.

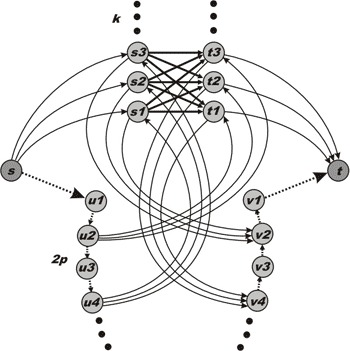
Пример графа, на котором алгоритм дает плохую асимптотику

«Грибок». Схема построения "сложного" для алгоритма Эдмондса-Карпа графа

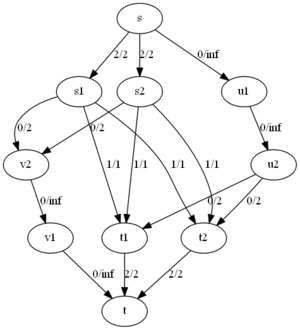
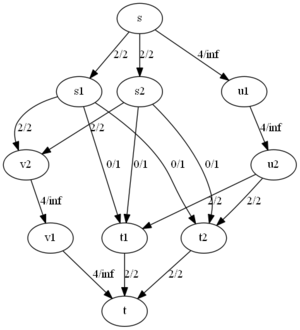
Заметим также, что существует сеть грибок на которой нижняя граница времени работы алгоритмы Эдмондса-Карпа также составляет $\Omega(V E^2)$. Рассмотрим этот случай более подробно. Норман Заде (англ. Norman Zadeh) описал примеры, которые позволяют добиться асимптотики $\Omega(V^3)$. В нашем примере алгоритм выполнит $\Omega(V^3)$ улучшений пути вне зависимости от выбора этого пути. Разделим все вершины (за исключением $s$ и $t$) на подмножества:

• $S={s_1,\ldots,s_k}$ — множество вершин, в которые входят рёбра из $s$ с пропускной способностью $k$,
• $T={t_1,\ldots,t_k}$ — множество вершин, из которых исходят рёбра в $t$ с пропускной способностью $k$,
• $U={u_1,\ldots,u_{2p}}$ — множество вершин, достижимых из $s$ по рёбрам с бесконечной пропускной способностью (не используя иные рёбра),
• $V={v_1,\ldots,v_{2p}}$ — множество вершин, из которых можно достигнуть $t$ по рёбрам с бесконечной пропускной способностью (не используя иные рёбра).

$S$ и $T$ содержат $k$ вершин, $U$ и $V$ содержат $2p$ вершин. Где $k$ и $p$ фиксированные целые числа. Каждое ребро, выделенное жирным(см. рисунок, соединяют множества $S$ и $T$), имеет единичную пропускную способность; пунктирные рёбра имеют бесконечную пропускную способность; остальные рёбра(в форме дуги) имеют пропускную способность $k$. В начале работы алгоритма путь увеличиться $k^2$ раз по пути ($s$, $S$, $T$, $t$), длина которого равна трем. После этого остаточная сеть будет содержать обратные рёбра из $T$ в $S$, и алгоритм выберет еще $k^2$ путей $(s, u_1, u_2, T, S, v_2, v_1, t)$ длины $7$, затем путь $(s, u_1, u_2, u_3, u_4, S, T, v_4, v_3, v_2, v_1, t)$ длины $11$ и так далее.

Число вершин в сети: $n = 2\cdot k + 4\cdot p + 2$.

Число рёбер: $m = k^2 + 2\cdot p\cdot k + 2\cdot k + 4\cdot p$.

Нетрудно заметить, что число удлиняющих путей $a = k^2\cdot (p+1)$. Возьмем $p$ равным $k - 1$. В этом случае $n = 6 \cdot k - 2$ и $a = k^3$. Заде приводит более хитрые примеры с такой же асимптотикой, но они зависят от выбора пути.

Изначальный граф, нулевой поток

Граф после $k^2$ поисков пути(в нашем случае $k^2 = 4$).
Рёбра из между множествами $S$ и $T$ полностью насыщены. Поток равен четырем

Алгоритм нашел путь через рёбра бесконечной вместимости, совершив еще $k^2 = 4$ шагов. Поток равен восьми

См. также

• Определение сети, потока
• Обход в ширину
• Алгоритм Форда-Фалкерсона

Источники информации

• Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)
• Википедия: Алгоритм Эдмондса-Карпа
• Википедия: Алгоритм Эдмондса-Карпа (англ.)
• Статья на TopCoder.com