Шифратор и дешифратор — различия между версиями
Gaporf (обсуждение | вклад) (→Источники информации) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 11 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | |||
{{Определение | {{Определение | ||
| − | |definition='''Шифратор''' (англ. ''encoder'') — логическая схема, имеющая <tex>2^n</tex> входов <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{2^n - 1}</tex> и <tex>n</tex> выходов <tex>z_0</tex>, <tex>z_1</tex>, <tex>\ldots</tex>, <tex>z_{n-1}</tex>. Если на <tex>i</tex>-ый вход <tex>s_i</tex> подать <tex>1</tex>, а на остальные входы — <tex>0</tex>, то выходы <tex>z_0</tex>, <tex>z_1</tex>, <tex>\ldots</tex>, <tex>z_{n-1}</tex> будут кодировать число <tex>i</tex>. | + | |definition='''Шифратор''' (англ. ''encoder'') — [[Реализация булевой функции схемой из функциональных элементов| логическая схема]], имеющая <tex>2^n</tex> входов <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{2^n - 1}</tex> и <tex>n</tex> выходов <tex>z_0</tex>, <tex>z_1</tex>, <tex>\ldots</tex>, <tex>z_{n-1}</tex>. Если на <tex>i</tex>-ый вход <tex>s_i</tex> подать <tex>1</tex>, а на остальные входы — <tex>0</tex>, то выходы <tex>z_0</tex>, <tex>z_1</tex>, <tex>\ldots</tex>, <tex>z_{n-1}</tex> будут кодировать число <tex>i</tex>. |
}} | }} | ||
{{Определение | {{Определение | ||
| − | |definition='''Дешифратор''' (англ. ''decoder'') — | + | |definition='''Дешифратор''' (англ. ''decoder'') — логическая схема, имеющая <tex>n</tex> входов <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex> и <tex>2^n</tex> выходов <tex>z_0</tex>, <tex>z_1</tex>, <tex>\ldots</tex>, <tex>z_{2^n-1}</tex>. На все выходы подаётся <tex>0</tex>, кроме выхода <tex>z_i</tex>, на который подаётся <tex>1</tex>, где <tex>i</tex> — число, которое закодировано входами <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex> |
}} | }} | ||
| Строка 14: | Строка 11: | ||
[[File:4-to-2encoder.png|thumb|180px|Шифратор 4-to-2]] | [[File:4-to-2encoder.png|thumb|180px|Шифратор 4-to-2]] | ||
| − | Принцип работы шифратора заключается в том, что выходы <tex>z_0</tex>, <tex>z_1</tex>, <tex>\ldots</tex>, <tex>z_{n-1}</tex> кодируют один из входов <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{2^n-1}</tex> в двоичной системе счисления. Очевидно, что если подать на несколько входов значение <tex>1</tex>, то такая схема будет работать некорректно. В качестве примера рассмотрим шифратор <tex>4</tex>-to-<tex>2</tex>. Если <tex>s_0 = 1</tex>, то <tex>z_0 = z_1 = 0</tex>, если же <tex>s_1 = 1</tex>, то <tex>z_0 = 1</tex> и <tex>z_1 = 0</tex>. Остальные случаи | + | Принцип работы шифратора заключается в том, что выходы <tex>z_0</tex>, <tex>z_1</tex>, <tex>\ldots</tex>, <tex>z_{n-1}</tex> кодируют один из входов <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{2^n-1}</tex> в двоичной системе счисления. Очевидно, что если подать на несколько входов значение <tex>1</tex>, то такая схема будет работать некорректно. В качестве примера рассмотрим шифратор <tex>4</tex>-to-<tex>2</tex>. Если <tex>s_0 = 1</tex>, то <tex>z_0 = z_1 = 0</tex>, если же <tex>s_1 = 1</tex>, то <tex>z_0 = 1</tex> и <tex>z_1 = 0</tex>. Остальные случаи разбираются аналогичным образом. |
{| class="wikitable" | {| class="wikitable" | ||
| Строка 42: | Строка 39: | ||
[[Файл:2to4decoder.png|thumb|180px|Дешифратор <tex>2</tex>-to-<tex>4</tex>]] | [[Файл:2to4decoder.png|thumb|180px|Дешифратор <tex>2</tex>-to-<tex>4</tex>]] | ||
| − | Суть дешифратора заключается в том, что с помощью <tex>n</tex> входов <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex> можно задавать выход, на который будет подаваться <tex>1</tex>. Для того, чтобы лучше понять, как работает дешифратор, рассмотрим в качестве примера дешифратор <tex>2</tex>-to-<tex>4</tex> (это значит, что у этого дешифратора есть два входа <tex>s_0</tex> и <tex>s_1</tex> и четыре выхода <tex>z_0</tex>, <tex>z_1</tex>, <tex>z_2</tex> и <tex>z_3</tex>). Если <tex>s_0 = s_1 = 0</tex>, то на выходе <tex>z_0</tex> будет значение <tex>1</tex>, на остальных выходах будет <tex>0</tex>. Если же <tex>s_0 = 1</tex>, <tex>s_1 = 0</tex>, то на выходе <tex>z_1</tex> будет <tex>1</tex>, на остальных выходах будут <tex>0</tex>. Если <tex>s_0 = 0</tex>, <tex>s _1 = 1</tex>, то на выходе <tex>z_2</tex> будет <tex>1</tex>, а на остальных входах будет <tex>0</tex>. Если же <tex>s_0 = s_1 = 1</tex>, то на выходе <tex>z_3</tex> будет <tex>1</tex>, а на других — <tex>0</tex> | + | Суть дешифратора заключается в том, что с помощью <tex>n</tex> входов <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex> можно задавать выход, на который будет подаваться <tex>1</tex>. Для того, чтобы лучше понять, как работает дешифратор, рассмотрим в качестве примера дешифратор <tex>2</tex>-to-<tex>4</tex> (это значит, что у этого дешифратора есть два входа <tex>s_0</tex> и <tex>s_1</tex> и четыре выхода <tex>z_0</tex>, <tex>z_1</tex>, <tex>z_2</tex> и <tex>z_3</tex>). Если <tex>s_0 = s_1 = 0</tex>, то на выходе <tex>z_0</tex> будет значение <tex>1</tex>, на остальных выходах будет <tex>0</tex>. Если же <tex>s_0 = 1</tex>, <tex>s_1 = 0</tex>, то на выходе <tex>z_1</tex> будет <tex>1</tex>, на остальных выходах будут <tex>0</tex>. Если <tex>s_0 = 0</tex>, <tex>s _1 = 1</tex>, то на выходе <tex>z_2</tex> будет <tex>1</tex>, а на остальных входах будет <tex>0</tex>. Если же <tex>s_0 = s_1 = 1</tex>, то на выходе <tex>z_3</tex> будет <tex>1</tex>, а на других — <tex>0</tex>. |
{| class="wikitable" | {| class="wikitable" | ||
| Строка 59: | Строка 56: | ||
==Логическая схема дешифратора== | ==Логическая схема дешифратора== | ||
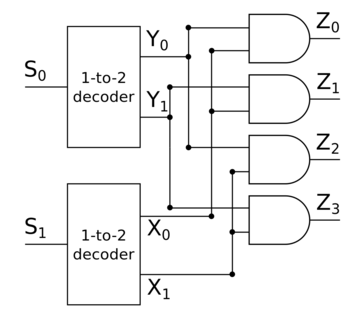
| − | Давайте построим логическую схему дешифратора рекурсивным способом: допустим, что мы построили схему для <tex>n-1</tex> входа, теперь попробуем слить <tex>n</tex>-ый выход с предыдущими <tex>n-1</tex>. Для <tex>n=1</tex> схема выглядит тривиальным образом: от входа <tex>s_0</tex> отходят два провода, один напрямую соединён с выходом <tex> | + | Давайте построим логическую схему дешифратора рекурсивным способом: допустим, что мы построили схему для <tex>n-1</tex> входа, теперь попробуем слить <tex>n</tex>-ый выход с предыдущими <tex>n-1</tex>. Для <tex>n=1</tex> схема выглядит тривиальным образом: от входа <tex>s_0</tex> отходят два провода, один напрямую соединён с выходом <tex>z_1</tex>, другой соединён с гейтом <tex>NOT</tex>, а гейт <tex>NOT</tex> соединён с выходом <tex>z_0</tex>. Теперь допустим, что мы можем построить схему для <tex>n-1</tex> входов. Тогда <tex>n</tex>-ый вход соединим с дешифратором <tex>1</tex>-to-<tex>2</tex>, а первые <tex>n-1</tex> входы соединим с дешифратором <tex>(n-1)</tex>-to-<tex>(2^{n-1})</tex> и потом соединим каждый выход дешифратора <tex>(n-1)</tex>-to-<tex>(2^{n-1})</tex> с каждым выходом дешифратора <tex>1</tex>-to-<tex>2</tex> с помощью гейтов <tex>AND</tex>, потом соединим соответствующие гейты с выходами <tex>z_i</tex> таким образом, чтобы значение на входе <tex>z_i</tex> было равно <tex>1</tex> только в том случае, если число <tex>i</tex> кодируется входами <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex>. Очевидно, что мы таким образом перебрали всевозможные комбинации значений на входах <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex>, поэтому наша схема будет работать верно. |
{| | {| | ||
| Строка 72: | Строка 69: | ||
*[[Реализация булевой функции схемой из функциональных элементов]] | *[[Реализация булевой функции схемой из функциональных элементов]] | ||
*[[Метод Лупанова синтеза схем]] | *[[Метод Лупанова синтеза схем]] | ||
| − | *[[Мультиплексор]] | + | *[[Мультиплексор и демультиплексор]] |
==Источники информации== | ==Источники информации== | ||
| − | *[https://en.wikipedia.org/wiki/Priority_encoder - Priority encoder] | + | *[https://en.wikipedia.org/wiki/Priority_encoder Wikipedia - Priority encoder] |
*[https://en.wikipedia.org/wiki/Binary_decoder Wikipedia - Binary decoder] | *[https://en.wikipedia.org/wiki/Binary_decoder Wikipedia - Binary decoder] | ||
*[https://www.efxkits.us/different-types-encoder-decoder-applications Different Types of Encoder and Decoder and Its Uses] | *[https://www.efxkits.us/different-types-encoder-decoder-applications Different Types of Encoder and Decoder and Its Uses] | ||
Текущая версия на 19:06, 4 сентября 2022
| Определение: |
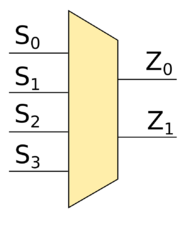
| Шифратор (англ. encoder) — логическая схема, имеющая входов , , , и выходов , , , . Если на -ый вход подать , а на остальные входы — , то выходы , , , будут кодировать число . |
| Определение: |
| Дешифратор (англ. decoder) — логическая схема, имеющая входов , , , и выходов , , , . На все выходы подаётся , кроме выхода , на который подаётся , где — число, которое закодировано входами , , , |
Содержание
[убрать]Принцип работы шифратора
Принцип работы шифратора заключается в том, что выходы , , , кодируют один из входов , , , в двоичной системе счисления. Очевидно, что если подать на несколько входов значение , то такая схема будет работать некорректно. В качестве примера рассмотрим шифратор -to-. Если , то , если же , то и . Остальные случаи разбираются аналогичным образом.
Логическая схема шифратора
Построить логическую схему шифратора можно следующим образом: давайте будем использовать гейт , который имеет входов (где — какое-то натуральное число), и на выходе возвращает , если на всех его входах будет подано , в противном случае этот гейт вернёт . Давайте рядом с каждым выходом поставим гейт , и будем, по необходимости, расширять этот гейт. Тогда для каждого входа рассмотрим двоичное представление номера этого входа, и если на -ом месте стоит , то соединим этот вход с гейтом , который соединён с выходом . Очевидно, если подать ровно на один вход , то выходы будут кодировать это число в двоичном представлении (если подать на вход , то на всех выходах будет , а сам вход не будет соединён ни с каким гейтом).
Принцип работы дешифратора
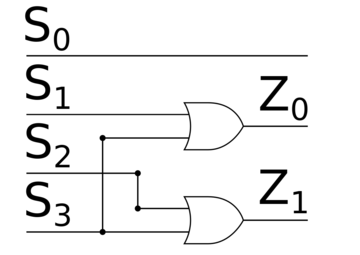
Суть дешифратора заключается в том, что с помощью входов , , , можно задавать выход, на который будет подаваться . Для того, чтобы лучше понять, как работает дешифратор, рассмотрим в качестве примера дешифратор -to- (это значит, что у этого дешифратора есть два входа и и четыре выхода , , и ). Если , то на выходе будет значение , на остальных выходах будет . Если же , , то на выходе будет , на остальных выходах будут . Если , , то на выходе будет , а на остальных входах будет . Если же , то на выходе будет , а на других — .
Логическая схема дешифратора
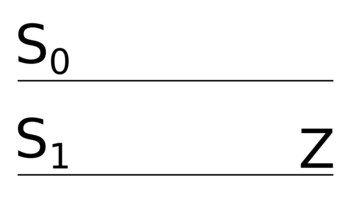
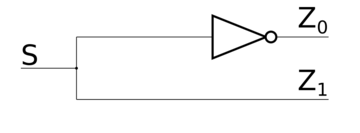
Давайте построим логическую схему дешифратора рекурсивным способом: допустим, что мы построили схему для входа, теперь попробуем слить -ый выход с предыдущими . Для схема выглядит тривиальным образом: от входа отходят два провода, один напрямую соединён с выходом , другой соединён с гейтом , а гейт соединён с выходом . Теперь допустим, что мы можем построить схему для входов. Тогда -ый вход соединим с дешифратором -to-, а первые входы соединим с дешифратором -to- и потом соединим каждый выход дешифратора -to- с каждым выходом дешифратора -to- с помощью гейтов , потом соединим соответствующие гейты с выходами таким образом, чтобы значение на входе было равно только в том случае, если число кодируется входами , , , . Очевидно, что мы таким образом перебрали всевозможные комбинации значений на входах , , , , поэтому наша схема будет работать верно.
Использование в реальной жизни
Принцип работы дешифратора используется при построении мультиплексора и демультиплексора. Также шифраторы и дешифраторы используются в том случае, когда надо передавать большое количество данных, при этом использовать много проводов затруднительно (к примеру телеграф). В этом случае они позволяют использовать малое количество проводов, обеспечивая при этом наибольшее возможное количество состояний, которое может быть передано.
См. также
- Реализация булевой функции схемой из функциональных элементов
- Метод Лупанова синтеза схем
- Мультиплексор и демультиплексор