Существенно неоднозначные языки

Неоднозначные грамматики

Неоднозначной грамматикой называется грамматика, по которой для одной цепочки существует более одного дерева разбора.

Пример:

Рассмотрим грамматику [math]E \rightarrow E + E | E * E[/math] и выводимую цепочку[math]E + E * E[/math]. Ее можно вывести двумя способами:

[math]E \Rightarrow E + E \Rightarrow E + E * E[/math]

[math]E \Rightarrow E * E \Rightarrow E + E * E[/math]

Эта граматика неоднозначна.

Существенно неоднозначные языки

Язык называется существенно неоднозначным, если любая его грамматика неоднозначна. Пример такого языка: [math]0^a 1^b 2^c[/math], где либо [math]a=b[/math], либо [math]b=c[/math] Докажем, что для любой грамматики [math]\Gamma[/math] [math]\exists k: 0^k 1^k 2^k[/math] имеет хотя бы 2 дерева разбора в грамматике [math]\Gamma[/math].

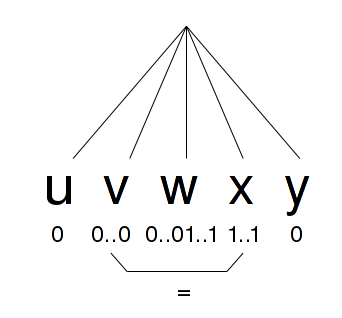
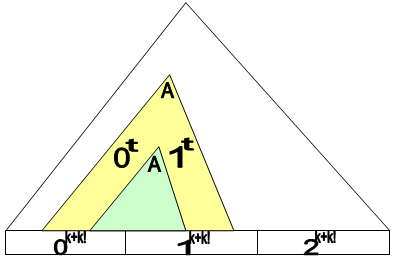
Возьмем k и рассмотрим слово [math]0^k 1^k 2^{k+k!}[/math], где пометим первые k нулей.

По лемме Огдена можно разбить данное слово на 5 частей.

По условию леммы есть нетерминал A - такой, что с помощью него можно породить слово [math]0^{k+k!} 1^{k+k!} 2^{k+k!}[/math].

[math]i = \frac{n!}{t} + 1[/math]

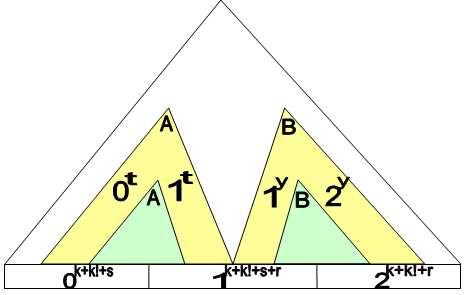
Аналогичные рассуждения справедливы для слова [math]0^{k+k!} 1^k 2^k[/math], в котором отмечены все двойки. Пусть в нем повторяющийся нетерминал B. [math]i = \frac{n!}{t} + 1[/math]

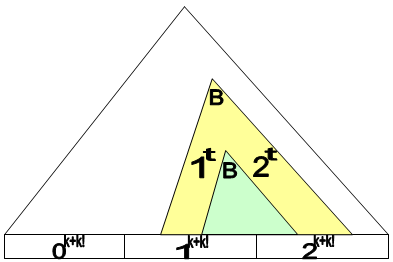
Очевидно, что А и В - разные деревья и одно не является потомком другого.

Тогда если дерево разбора в обоих случаях одинаково, то оно порождает слово вида [math]0^{k+k!+s} 1^{k+k!+s+r} 2^{k+k!+r}[/math], что не так.

В результате мы имеем 2 дерева разбора для одного слова. Значит язык существенно не однозначен.

Теорема:

Для языка принимаемого ДМП-автоматом существует однозначная КС-грамматика