Виды ансамблей

Ансамбль

Рассмотрим задачу классификации на K классов: [math]Y = \{1, 2, ..., K\}[/math]
Пусть имеется M классификатор ("экспертов"): [math] f_1, f_2, ..., f_M [/math]
[math] f_m : X \leftarrow Y, f_m \in F, m = (1 ... M) [/math]

Тогда давайте посмотрим новый классификатор на основе данных:

Простое голосование: [math] f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M I(f_i(x) = k) [/math]
Взвешенное голосование: [math] f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M \alpha_i I(f_i(x) = k), \sum \limits_i \alpha_i = 1, \alpha_i \gt 0[/math]

Теорема Кондорсе о присяжных

Теорема:

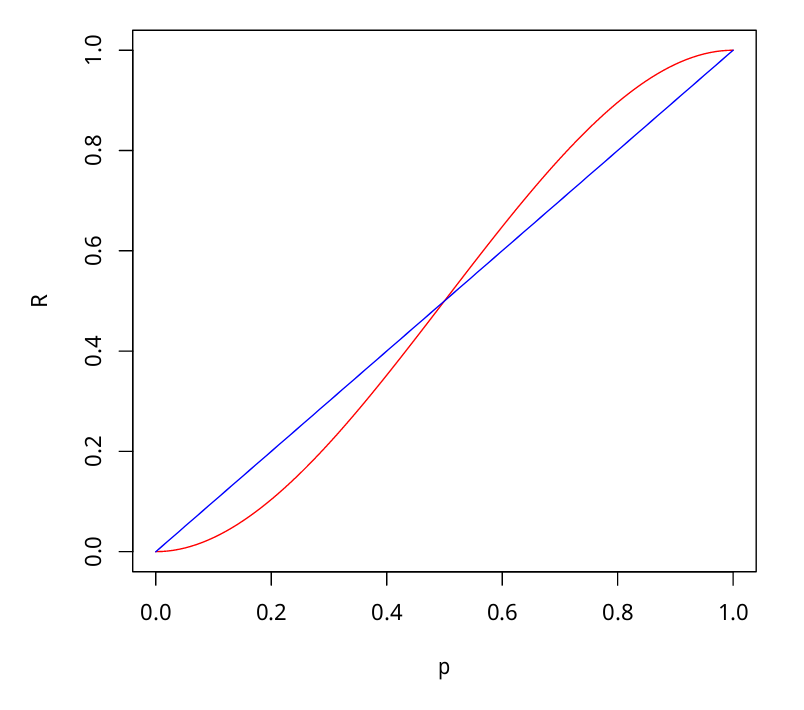
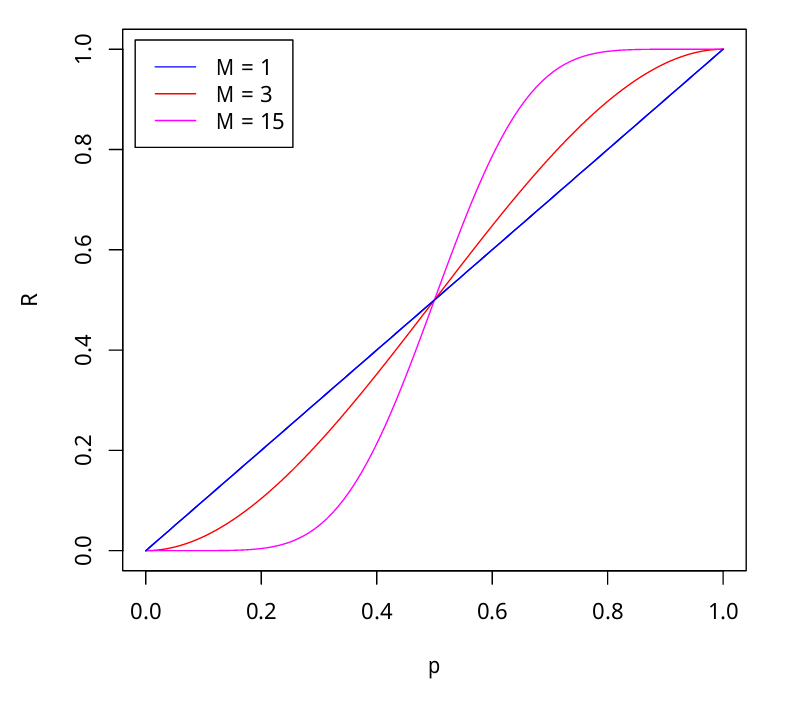
Если каждый член жюри присяжных имеет независимое мнение, и если вероятность правильного решения члена жюри больше 0.5, то тогда вероятность правильного решения присяжных в целом возрастает с увеличением количества членов жюри, и стремиться к единице. Если же вероятность быть правым у каждого из членов жюри меньше 0.5, то вероятность принятия правильного решения присяжными в целом монотонно уменьшается и стремится к нулю с увеличением количества присяжных.

Пусть [math]M[/math] - количество присяжный, [math]p[/math] - вероятность правильного решения одного эксперта, [math]R[/math] - вероятность правильного решения всего жюри, [math]m[/math] - минимальное большинство членов жюри [math] = \lfloor \frac N 2 \rfloor + 1 [/math]

Тогда [math] R = \sum \limits_{i = m}^M C_M^i p ^ i (1 - p) ^ {M - i} [/math]

Бутстрэп

Метод бутстрэпа (англ. bootstrap) — один из первых и самых простых видов ансамблей, который позволяет оценивать многие статистики сложных распределений и заключается в следующем. Пусть имеется выборка [math]X[/math] размера [math]N[/math]. Равномерно возьмем из выборки [math]N[/math] объектов с возвращением. Это означает, что мы будем [math]N[/math] раз равновероятно выбирать произвольный объект выборки, причем каждый раз мы выбираем из всех исходных [math]N[/math] объектов. Отметим, что из-за возвращения среди них окажутся повторы.
Обозначим новую выборку через [math]X_1[/math]. Повторяя процедуру [math]M[/math] раз, сгенерируем [math]M[/math] подвыборок [math]X_1 ... X_M[/math]. Теперь мы имеем достаточно большое число выборок и можем оценивать различные статистики исходного распределения.

Бутстрэп используется в статистике, в том числе для:

• Аппроксимация стандартной ошибки выборочной оценки
• Байесовская коррекция с помощью Бутстрэп метода
• Доверительные интервалы
• Метод процентилей

Бэггинг

Пусть имеется выборка [math]X[/math] размера [math]N[/math]. Количество классификаторов [math]M[/math]

Алгоритм классификации в технологии бэггинг на подпространствах:

• Генерируется с помощью бутстрэпа M выборок размера N для каждого классификатора
• Производится независимое обучения каждого элементарного классификатора (каждого алгоритма, определенного на своем подпространстве).
• Производится классификация основной выборки на каждом из подпространств (также независимо).
• Принимается окончательное решение о принадлежности объекта одному из классов. Это можно сделать несколькими разными способами, подробнее описано ниже.

Окончательное решение о принадлежности объекта классу может приниматься, например, одним из следующих методов:

• Консенсус: если все элементарные классификаторы присвоили объекту одну и ту же метку, то относим объект к выбранному классу.
• Простое большинство: консенсус достижим очень редко, поэтому чаще всего используют метод простого большинства. Здесь объекту присваивается метка того класса, который определило для него большинство элементарных классификаторов.
• Взвешивание классификаторов: если классификаторов четное количество, то голосов может получиться поровну, еще возможно, что для эксперты одна из групп параметров важна в большей степени, тогда прибегают к взвешиванию классификаторов. То есть при голосовании голос классификатора умножается на его вес.

Примеры кода

Инициализация

   #Импорты
   from pydataset import data

   #Считаем данные The Boston Housing Dataset
   df = data('Housing')
   
   #Проверим данные
   df.head().values
   array([[42000.0, 5850, 3, 1, 2, 'yes', 'no', 'yes', 'no', 'no', 1, 'no'],
          [38500.0, 4000, 2, 1, 1, 'yes', 'no', 'no', 'no', 'no', 0, 'no'],
          [49500.0, 3060, 3, 1, 1, 'yes', 'no', 'no', 'no', 'no', 0, 'no'], ...

   # Создадим словарь для слов 'no', 'yes'
   d = dict(zip(['no', 'yes'], range(0,2)))
   for i in zip(df.dtypes.index, df.dtypes):
       if str(i[1]) == 'object':
           df[i[0]] = df[i[0]].map(d)
   df[‘price’] = pd.qcut(df[‘price’], 3, labels=[‘0’, ‘1’, ‘2’]).cat.codes

   # Разделим множество на два
   y = df['price'] 
   X = df.drop('price', 1)

Бэггинг

   # Импорты классификаторов
   from sklearn.model_selection import cross_val_score
   from sklearn.ensemble import BaggingClassifier, ExtraTreesClassifier, RandomForestClassifier
   from sklearn.neighbors import KNeighborsClassifier
   from sklearn.linear_model import RidgeClassifier
   from sklearn.svm import SVC

   seed = 1075
   np.random.seed(seed)
   # Инициализуруем классификаторы
   rf = RandomForestClassifier()
   et = ExtraTreesClassifier()
   knn = KNeighborsClassifier()
   svc = SVC()
   rg = RidgeClassifier()
   clf_array = [rf, et, knn, svc, rg]
   for clf in clf_array:
       vanilla_scores = cross_val_score(clf, X, y, cv=10, n_jobs=-1)
       bagging_clf = BaggingClassifier(clf, max_samples=0.4, max_features=10, random_state=seed)
       bagging_scores = cross_val_score(bagging_clf, X, y, cv=10, n_jobs=-1)
       print "Mean of: {1:.3f}, std: (+/-) {2:.3f [{0}]"  
                          .format(clf.__class__.__name__, 
                          vanilla_scores.mean(), vanilla_scores.std())
       print "Mean of: {1:.3f}, std: (+/-) {2:.3f} [Bagging {0}]\n"
                          .format(clf.__class__.__name__, 
                           bagging_scores.mean(), bagging_scores.std())

   #Результат
   Mean of: 0.632, std: (+/-) 0.081 [RandomForestClassifier]
   Mean of: 0.639, std: (+/-) 0.069 [Bagging RandomForestClassifier]
   Mean of: 0.636, std: (+/-) 0.080 [ExtraTreesClassifier]
   Mean of: 0.654, std: (+/-) 0.073 [Bagging ExtraTreesClassifier]
   Mean of: 0.500, std: (+/-) 0.086 [KNeighborsClassifier]
   Mean of: 0.535, std: (+/-) 0.111 [Bagging KNeighborsClassifier]
   Mean of: 0.465, std: (+/-) 0.085 [SVC]
   Mean of: 0.535, std: (+/-) 0.083 [Bagging SVC]
   Mean of: 0.639, std: (+/-) 0.050 [RidgeClassifier]
   Mean of: 0.597, std: (+/-) 0.045 [Bagging RidgeClassifier]

Источники информации

• https://medium.com/@rrfd/boosting-bagging-and-stacking-ensemble-methods-with-sklearn-and-mlens-a455c0c982de
• https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html