Контексты и синтаксические моноиды

Контексты

Правый контекст

Определение:

Правым контекстом (англ. right context) [math]C_L^R(y)[/math] слова [math]y[/math] в языке [math]L[/math] называется множество [math]\{z \mid yz \in L\}[/math].

Лемма:

Язык [math]L[/math] — регулярный [math]\Leftrightarrow[/math] множество [math]\{C_L^R(y) \mid y \in \Sigma^*\}[/math] его правых контекстов конечно.

Доказательство:

[math]\triangleright[/math]

Автомат на правых контекстах. Легенда: начальное / промежуточное / дьявольское / терминальное состояния; контекст [math]\Leftarrow[/math] Пусть множество правых контекстов языка конечно. Построим распознающий его автомат. Состояния автомата будут соответствовать различным правым контекстам. Таким образом, каждая вершина автомата соответствует множеству допустимых «продолжений» считанного на данный момент слова. Переход по некоторому символу из одного состояния в другое осуществляется, если контекст, соответствующий первому состоянию, содержит все элементы, которые получаются приписыванием этого символа в начало элементам контекста, соответствующего второму. Вершина, соответствующая контексту пустого слова, является стартовой ([math]C_L^R(\varepsilon) = L[/math]). Вершины, контексты которых содержат [math]\varepsilon[/math], должны быть допускающими. Покажем что полученный автомат допускает в точности указанный язык. Выпишем свойства, которые мы стремились удовлетворить при построении: 1. [math] u \quad \leftrightarrow \quad C_L^R(x) ,\ v \quad \leftrightarrow \quad C_L^R(xc) \quad \Leftrightarrow \quad \langle u,c \rangle \vdash \langle v, \varepsilon \rangle [/math] 2. [math] s \quad \leftrightarrow \quad C_L^R(\varepsilon) [/math], где [math] s [/math] — стартовое состояние. 3. [math] \varepsilon \in C_L^R(\omega) \quad \Leftrightarrow \quad v \in T \quad ( v \quad \leftrightarrow \quad C_L^R(\omega) ) [/math] Из 1 следует 1*. [math] u \quad \leftrightarrow \quad C_L^R(x) ,\ v \quad \leftrightarrow \quad C_L^R(x \omega) \quad \Leftrightarrow \quad \langle u,\omega \rangle \vdash^* \langle v, \varepsilon \rangle [/math] Положив [math] s = u [/math] и учтя 2, получим [math] v \quad \leftrightarrow \quad C_L^R(\omega) \quad \Leftrightarrow \quad \langle s,\omega \rangle \vdash^* \langle v, \varepsilon \rangle [/math] Теперь зафиксируем за состоянием [math] v [/math] контекст [math] C_L^R(\omega) [/math]. Тогда левая часть 3 равносильна [math] \omega \in L [/math], а правая, с учётом [math] \langle s,\omega \rangle \vdash^* \langle v, \varepsilon \rangle [/math], означает, что автомат допускает [math] \omega [/math]. [math]\Rightarrow[/math] Пусть [math]L[/math] — регулярный. В таком случае существует автомат [math]\mathcal{A}[/math], распознающий его. Рассмотрим произвольное слово [math]y[/math]. Положим [math]u[/math] — такое состояние [math]\mathcal{A}[/math], в которое можно перейти из начального по слову [math]y[/math]. Тогда [math]C_L^R(y)[/math] совпадает с множеством слов, по которым из состояния [math]u[/math] можно попасть в допускающее. Причем если по какому-то слову [math]z[/math] тоже можно перейти из начального состояния в [math]u[/math], то [math]C_L^R(y) = C_L^R(z)[/math]. Наоборот, если [math]C_L^R(y) = C_L^R(z)[/math], то состояния, в которые можно перейти по словам [math]y[/math] и [math]z[/math], эквивалентны. Таким образом, можно установить взаимное соответствие между правыми контекстами и классами эквивалентности вершин автомата, которых конечное число.

[math]\triangleleft[/math]

Примеры

Здесь будем понимать под [math] C_L^R(X) = Y [/math] не стандартное отображение множества в множество, а [math] \forall x \in X :\ C_L^R(x) = Y [/math]. Рассмотрим правые контексты следующих языков:

Автомат к языку [math] \{ 001, 111, 100 \} [/math]

1. [math] \{ 001, 111, 100 \} [/math]

   Возникающие контексты:

   1. [math] C_L^R(\varepsilon) = \{ 001, 111, 100 \} [/math]
      
      
   2. [math] C_L^R(0) = \{ 01 \} [/math]
      
      
   3. [math] C_L^R(00) = \{ 1 \} [/math]
      
      
   4. [math] C_L^R(001) = \{ \varepsilon \} [/math]
      
      
   5. [math] C_L^R(1) = \{ 11, 00 \} [/math]
      
      
   6. [math] C_L^R(10) = \{ 0 \} [/math]
      
      
   7. [math] C_L^R(100) = \{ \varepsilon \} [/math]
      
      
   8. [math] C_L^R(11) = \{ 1 \} [/math]
      
      
   9. [math] C_L^R(111) = \{ \varepsilon \} [/math]
      
      
   10. [math] C_L^R(X) = \varnothing [/math], где [math] X [/math] — множество остальных аргументов.
       
       

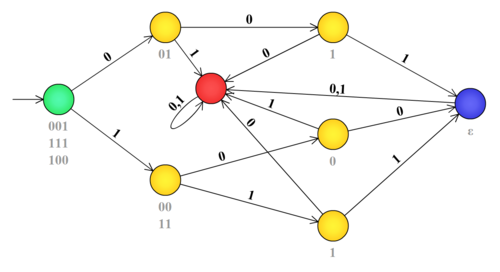
   Начальное состояние — 1 . Допускающие состояния: 4, 7, 9 (в них [math] \varepsilon \in C_L^R(...) [/math]). Состояние 10 — дьявольское. Всего 8 состояний (именно столько имеется различных контекстов).

   

   Автомат к языку [math] 0^*11 [/math]

2. [math] 0^*11 [/math]

   Возможные контексты (аргументы упорядочены в лексикографическом порядке):

   1. [math] C_L^R(0^*) = 0^*11 [/math]
      
      
   2. [math] C_L^R(0^*1) = 1 [/math]
      
      
   3. [math] C_L^R(0^*10(0|1)^*) = \varnothing [/math]
      
      
   4. [math] C_L^R(0^*11) = \varepsilon [/math]
      
      
   5. [math] C_L^R(0^*11(0|1)^+) = \varnothing [/math]
      
      

   Итого 4 состояния; начальное состояние 1, допускающее 4, состояние 3&5 — дьявольское.

Левый контекст

Определение:

Левым контекстом (англ. left context) [math]C_L^L(y)[/math] слова [math]y[/math] в языке [math]L[/math] называется множество [math]\{z \mid zy \in L\}[/math].

Лемма:

Язык [math]L[/math] — регулярный [math]\Leftrightarrow[/math] множество [math]\{C_L^L(y) \mid y \in \Sigma^*\}[/math] его левых контекстов конечно.

Доказательство:

[math]\triangleright[/math]

Поскольку множество регулярных языков замкнуто относительно операции разворота, то из того, что [math]C_L^L(y) = \overleftarrow{C_{\overleftarrow{L}}^R(\overleftarrow{y})}[/math] и аналогичного утверждения о правых контекстах получаем требуемое.

[math]\triangleleft[/math]

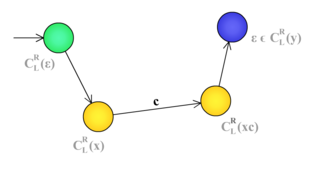
Двухсторонний контекст

Определение:

Двухсторонним контекстом (англ. two-sided context) [math]C_L(y)[/math] слова [math]y[/math] в языке [math]L[/math] называется множество [math]\{\langle x,z\rangle \mid xyz \in L\}[/math].

Любопытное замечание: [math]C_L(\varepsilon)[/math] состоит из всех пар строк, которые при конкатенации дают слово из языка.

Для доказательства последующих утверждений будем использовать бинарное отображение [math] (\cdot) :\ Q \times \Sigma^* \rightarrow Q [/math] со свойством [math] q \cdot \omega = q' \Leftrightarrow \langle q,\omega \rangle \vdash^* \langle q', \varepsilon \rangle[/math].

Лемма:

Язык [math]L[/math] — регулярный [math]\Leftrightarrow[/math] множество [math]\{C_L(y) \mid y \in \Sigma^*\}[/math] его двухсторонних контекстов конечно.

Доказательство:

[math]\triangleright[/math]

[math]\Leftarrow[/math] Заметим, что [math] \{ z \mid \langle \varepsilon, z \rangle \in C_L(y) \} = C_L^R(y) [/math]. Следовательно, если множество двухсторонних контекстов языка конечно, то конечно и множество его правых контекстов, а это значит, что язык регулярный. [math]\Rightarrow[/math] Пусть [math]L[/math] — регулярный. В таком случае существует детерминированный автомат [math]\mathcal{A}[/math], распознающий его. Понятно, что для любого слова [math] xyz [/math], допускаемого автоматом, существуют [math] u ,\ v [/math] такие, что [math] s \cdot x = u ,\ u \cdot y = v ,\ v \cdot z \in T [/math] (где [math] s [/math] — начальное состояние). Тогда справедливо равенство [math] C_L(y) = \bigcup\limits_{(u, v) :\ u \cdot y = v} \{ \langle x, z \rangle \mid s \cdot x = u ,\ v \cdot z \in T \} [/math]. Учитывая [math] | \{ (u, v) \mid u,v \in Q \} | = |Q|^2 [/math], получаем [math] | \{ C_L(y) \mid y \in \Sigma^* \} | \leqslant 2^{|Q|^2} [/math], то есть множество контекстов конечно.

[math]\triangleleft[/math]

Синтаксический моноид

Определения

Определение:

Синтаксическим моноидом (англ. syntactic monoid) [math]M(L)[/math] языка [math]L[/math] называется множество, состоящее из его классов эквивалентности [math][[x]] = \{ y \in \Sigma^* \mid C_L(x) = C_L(y) \}[/math], с введённым на нём операцией конкатенации [math]\circ[/math], где [math][[x]]\circ[[y]] = [[xy]][/math]. Нейтральным элементом в нём является [math][[\varepsilon]][/math].

Определение:

Групповой язык (англ. group language) — это язык, синтаксический моноид которого является группой.

Свойства

Синтаксический моноид [math]M(L)[/math] определён для любого [math]L \in \Sigma^*[/math], однако некоторые свойства языка можно определить по структуре его синтаксического моноида. Размер синтаксического моноида является мерой структурной сложности языка.

Теорема:

Язык [math]L[/math] — регулярный [math]\Leftrightarrow[/math] его синтаксический моноид [math]M(L)[/math] конечен.

Доказательство:

[math]\triangleright[/math]

Размер синтаксического моноида [math]M(L)[/math] языка [math]L[/math] равен количеству его различных двухсторонних контекстов [math]C_L[/math]. Применяя лемму, доказанную ранее, получаем: Язык [math]L[/math] — регулярный [math]\Leftrightarrow[/math] множество [math]\{C_L(y) \mid y \in \Sigma^*\}[/math] его двухсторонних контекстов конечно [math]\Leftrightarrow[/math] его синтаксический моноид [math]M(L)[/math] конечен.

[math]\triangleleft[/math]

Лемма:

Пусть язык [math]L[/math] распознается ДКА [math]\mathcal{A} = \langle \Sigma,Q,s,T,\delta \rangle[/math]. Тогда размер его синтаксического моноида [math]M(L)[/math] не превосходит [math]|Q|^{|Q|}[/math].

Доказательство:

[math]\triangleright[/math]

Введём следующее отношение эквивалентности на строках: [math]x \cong y \Leftrightarrow \forall q \in Q: q \cdot x = q \cdot y[/math] Оценим количество классов, на которые отношение [math]\cong[/math] разбивает язык [math]L[/math]. Для этого пронумеруем состояния, и каждому слову [math] \omega[/math] сопоставим вектор [math] a_{\omega} \in Q^{|Q|} [/math] такой, что [math] a_{\omega}[i] = q_j \Leftrightarrow q_i \cdot \omega = q_j [/math]. Количество различных таких векторов — [math] {|Q|}^{|Q|} [/math]. В то же время неэквивалентным словам соответствуют разные [math] a [/math], тогда количество классов эквивалентности также ограничено [math] {|Q|}^{|Q|} [/math]. Остаётся показать, что существует взаимно-однозначное соответствие между нашими классами эквивалентности и синтаксическими моноидами. Смотрим: [math] x \cong y [/math] [math] \Leftrightarrow [/math] [math] s \cdot (uxv) = ((s \cdot u) \cdot x) \cdot v = ((s \cdot u) \cdot y) \cdot v = s \cdot (uyv) [/math] (пусть [math] s \cdot u [/math] равно [math] q [/math] из определения [math] \cong [/math], тогда [math] (s \cdot u) \cdot x = q \cdot x = q' = q \cdot y = (s \cdot u) \cdot y [/math]) [math] \Leftrightarrow [/math] [math] s \cdot (uxv) \in T \Leftrightarrow s \cdot (uyv) \in T [/math] [math] \Leftrightarrow [/math] [math] uxv \in L \Leftrightarrow uyv \in L [/math] [math] \Leftrightarrow [/math] [math] [[x]] = [[y]] [/math] ([math] s [/math] — начальное состояние).

[math]\triangleleft[/math]

Пусть [math]\mathcal{A} = \langle \Sigma,Q,s,T,\delta \rangle[/math] — ДКА. Каждое слово [math]\omega \in \Sigma^*[/math] порождает отображение [math]f_\omega : Q \rightarrow Q[/math], определённое следующим образом: [math]f_\omega(q) = q \cdot \omega[/math].

Определение:

Моноидом переходов (англ. transition monoid) [math]M(\mathcal{A})[/math] называется множество отображений [math]f_\omega[/math] с операцией композиции. [math]f_x \cdot f_y = f_{xy}[/math]. Нейтральным элементом в данном моноиде является отображение [math]f_\varepsilon[/math].

Теорема:

Пусть [math]\mathcal{A} = \langle \Sigma,Q,s,T,\delta \rangle[/math] — минимальный ДКА, задающий язык [math]L[/math]. Тогда [math]M(\mathcal{A})[/math] и [math]M(L)[/math] изоморфны.

Доказательство:

[math]\triangleright[/math]

Покажем, что [math]f_x = f_y \quad \Leftrightarrow \quad [[x]] = [[y]][/math]. [math]\Rightarrow[/math] Данный факт был показан в доказательстве предыдущей леммы, он не требует минимальности автомата. [math]\Leftarrow[/math] Пусть [math][[x]] = [[y]][/math] и [math]q \in Q[/math]. Тогда [math]q = s \cdot u[/math] для некоторого слова [math]u[/math]. Пусть [math]q_1 = f_x(q) = s \cdot ux[/math] и [math]q_2 = f_y(q) = s \cdot uy[/math]. Поскольку [math][[x]] = [[y]][/math], справедливо [math]uxv \in L \quad \Leftrightarrow \quad uyv \in L[/math]. Следовательно, [math]q_1 \cdot v \in T \Leftrightarrow q_2 \cdot v \in T[/math], то есть [math]q_1[/math] и [math]q_2[/math] эквивалентны. Значит, [math]q_1 = q_2[/math], так как автомат [math]\mathcal{A}[/math] минимален. То есть, [math]f_x = f_y[/math].

[math]\triangleleft[/math]

Примеры

1. Рассмотрим язык [math]L = \{\omega \mid |\omega| \bmod 2 = 0 \}[/math].

[math]\{\langle u, v \rangle \mid uxv \in L\}[/math] — это множество всех пар [math]\langle u,v \rangle[/math], таких что [math]|u| + |v| = |x|[/math] [math](mod[/math] [math]2)[/math].

Значит, [math]M(L)[/math] состоит из двух элементов: множества слов чётной длины и множества слов нечётной длины. Нейтральным элементом в данном моноиде является множество слов чётной длины.

Оба элемента являются обратными самим себе, значит [math]M(L)[/math] является группой, следовательно [math]L[/math] — групповой язык.

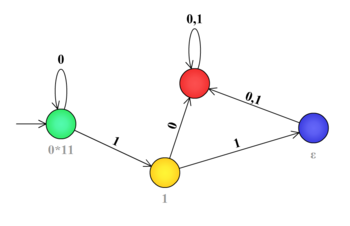
2. Язык [math]L[/math] над алфавитом [math]\Sigma = \{0,1\}[/math] задан регулярным выражением [math]1(0|1)^*[/math]. Его синтаксический моноид [math]M(L)[/math] содержит три элемента:

a) [math][[\varepsilon]][/math] — нейтральный элемент. Включает в себя только пустую строку.

b) [math][[0]][/math] содержит все строки, распознаваемые регулярным выражением [math]0(0|1)^*[/math]. [math]\forall x \in [[0]]: C_L(x) = \{\langle u, v \rangle \mid u \in L, v \in \Sigma^* \}[/math].

c) [math][[1]][/math] содержит все строки, принадлежащие языку, то есть, распознаваемые регулярным выражением [math]1(0|1)^*[/math]. [math]\forall x \in [[1]]: C_L(x) = C_L(\varepsilon) \cup \{\langle \varepsilon, v \rangle \mid v \in \Sigma^* \}[/math].

Заметим, что [math][[0]][/math] и [math][[1]][/math] не имеют обратных элементов в данном моноиде, так как нейтральный элемент содержит только пустую строку, а её невозможно получить из непустой с помощью конкатенации. Следовательно [math]L[/math] не является групповым языком.

3. Язык [math]L = 0^n1^n[/math] задан над алфавитом [math]\Sigma = \{0,1\}[/math].

Балансом слова [math]|\omega|_b[/math] назовём число, равное разности между количеством нулей и единиц, встречающихся в данном слове. Если слово [math]\omega = uxv[/math] принадлежит языку [math]L[/math], то [math]|x|_b = -(|u|_b + |v|_b)[/math]. Но [math]|x|_b[/math] может принимать любое целое значение, при том, что [math]x[/math] имеет непустой двухсторонний контекст.

Значит, синтаксический моноид [math]M(L)[/math] имеет бесконечное количество элементов, что значит, что данный язык не является регулярным.

Источники информации

• Howard Straubing Finite automata, formal logic, and circuit complexity, 1994. ISBN 3-7643-3719-2. — C. 53.
• James A. Anderson Automata theory with modern applications, 2006. ISBN 0-521-61324-8. — С. 72.
• Wikipedia — Syntactic monoid