Укладка графа на плоскости

Пример планарного графа. Синим контуром обозначены грани, за исключением внешней грани (всего 5 граней). Обратите внимание, что внутри грани могут содержаться другие ребра и вершины.

Определение: Граф обладает укладкой в пространстве [math]L[/math], если он изоморфен графу, вершинами которого являются некоторые точки пространства, а ребрами — жордановы кривые , соединяющие соответствующие вершины, причем Кривая, являющаяся ребром не проходит через другие вершины графа, кроме вершин, которые она соединяет; Две кривые, являющиеся ребрами, пересекаются лишь в вершинах, инцидентных одновременно обоим этим ребрам. Соответствующий граф, составленный из точек пространства и жордановых кривых из [math]L[/math], называют укладкой исходного графа. Определение: Граф называется планарным (англ. planar graph), если он обладает укладкой на плоскости. Плоским (англ. plane graph, planar embedding of the graph) называется граф уже уложенный на плоскости.

Определение: Плоский граф разбивает плоскость на несколько областей, называемых гранями (англ. faces). Одна из граней не ограничена, ее называют внешней (англ. external) гранью, а остальные — внутренними (англ. unbounded) гранями. Для плоских графов есть простое соотношение, называемое формулой Эйлера: [math]V - E + F = 2[/math], где [math]V[/math] — вершины, [math]E[/math] — ребра, [math]F[/math] — грани. Это свойство позволяет в некоторых случаях просто доказывать непланарность некоторых графов, например непланарность [math]K_5[/math] и [math]K_{3,3}[/math]. Понятно, что любой граф, содержащий подграф [math]K_5[/math] или [math]K_{3,3}[/math] непланарен. Оказывается, верно и обратное утверждение, но для его формулировки потребуется вспомогательное определение:

Полный двудольный граф [math]K_{3,3}[/math]. Этот граф непланарен, и его не получится изобразить на плоскости без пересечений ребер.

Определение:

Введем отношение [math]R[/math] следующим образом: два графа на находятся в отношении [math]R[/math], если один можно свести к другому заменой вершины степени 2 на ребро между вершинами смежными ей, или наоборот, добавлением вершины степени два на ребро (см. картинку). Отношением гомеоморфизма (или топологической эквивалентности) назовем транзитивное замыкание отношения [math]R[/math]: [math]R[/math]*.

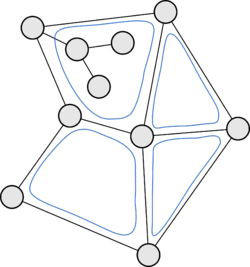
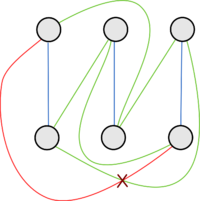
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных [math]K_5[/math] и [math]K_{3,3}[/math]: теорема Понтрягина-Куратовского.

Теорема:

В трехмерном евклидовом пространстве любой граф укладывается.

Доказательство:

[math]\triangleright[/math]

Все вершины произвольного графа [math]G[/math] помещаем в различных точках координатной оси [math]OX[/math]. Рассмотрим пучок плоскостей, проходящих через ось [math]OX[/math], и зафиксируем [math]|E|[/math] различных таких плоскостей. Теперь каждое ребро [math](u, v)[/math] изобразим полуокружностью, проходящей в соответствующей плоскости через вершины [math]u, v[/math]. Ясно, что различные ребра не будут пересекаться кроме как в общих вершинах.

[math]\triangleleft[/math]

См. также

• Формула Эйлера
• Локализация в ППЛГ методом полос (персистентные деревья)

Источники информации

• Асанов М, Баранский В., Расин В. - Дискретная математика - Графы, матроиды, алгоритмы
• Харари, Ф. Теория графов. — М.: Книжный дом «ЛИБРОКОМ», 2009. — С. 126. — ISBN 978­-5­-397­-00622­-4.