Теорема Понтрягина-Куратовского

Теорема:

Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных [math] K_{5} [/math], и не содержит подграфов, гомеоморфных [math] K_{3, 3} [/math] .

Доказательство:

[math]\triangleright[/math]

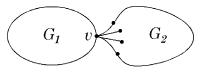
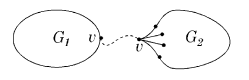
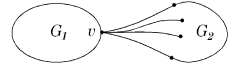
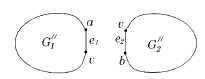
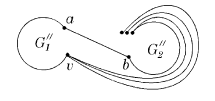
Необходимость Необходимость условия очевидна. Достаточность От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных [math] K_{5} [/math] или [math] K_{3, 3} [/math]. Пусть [math] G [/math] - такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. G связен Если [math] G [/math] не связен, то его компоненты связности планарны и, следовательно, сам граф [math] G [/math] планарен. G - обыкновенный граф В самом деле, пусть в графе [math] G [/math] есть петля или кратное ребро [math] e [/math]. Тогда граф [math] G - e [/math] планарен. Добавляя ребро [math] e [/math] к графу [math] G - e [/math] получим, что граф [math] G [/math] он планарен. G - блок Пусть, от противного, в графе есть точка сочленения [math] v [/math]. Через [math] G_1 [/math] обозначим подграф графа [math] G [/math], порождённый вершинами одной из компонент связности графа [math] G - v[/math] и вершинной [math] v [/math], а через [math] G_2 [/math] подграф графа [math] G [/math], порождённый вершинами остальных компонент связности графа [math] G - v [/math] и вершиной [math] v [/math]. (рис. 1) рис. 1 Возьмём укладку графа [math] G_1 [/math] на плоскости такую, что вершина [math] v [/math] лежит на границе верхней грани. Затем во внешней грани графа [math] G_1 [/math] возьмём укладку графа [math] G_2 [/math] такую, что вершина [math] v [/math] будет представлена на плоскости в двух экземплярах. (рис. 2) рис. 2 Соединим два экземпляра вершины [math] v [/math] пучком жордановых линий, не допуская лишних пересечений с укладками графов [math] G_1 [/math] и [math] G_2 [/math], состоящим из такого количества линий, какова степень вершины [math] v [/math] в графе [math] G_2 [/math]. Далее отбросим вхождение вершины [math] v [/math] в граф [math] G_2 [/math], заменяя инцидентные её рёбра на жордановы линии, полученные из линий указанного пучка и рёбер (рис. 3) рис. 3 Таким образом мы получили укладку графа [math] G [/math] на плоскости, что невозможно. Пусть [math] e = ab [/math] - произвольное ребро графа [math] G [/math], [math] G' = G - e [/math]. граф [math] G' [/math] планарен в силу минимальности графа [math] G [/math]. граф [math] G' [/math] связен в силу отсутствия в графе [math] G [/math] мостов. В G' существует цикл, содержащий вершины a и b Пусть [math] a [/math] и [math] b [/math] лежат в одном блоке [math] B [/math] графа [math] G' [/math]. Если [math] |VB| \gt = 3 [/math], то существует цикл графа G', содержащий вершины [math] a [/math] и [math] b [/math]. Если [math] |VB| = 2 [/math], то в [math] B [/math] имеется ребро [math] e' = ab [/math], но тогда в [math] G [/math] имеются кратные рёбра [math] e [/math] и [math] e' [/math], что невозможно. Если вершины [math] a [/math] и [math] b [/math] лежат в разных блоках графа [math] G' [/math], что существует точка сочленения [math] v [/math], принадлежащая любой простой (a, b)-цепи графа [math] G' [/math]. Через [math] G'_1 [/math] обозначим подграф графа [math] G' [/math], порождённый вершиной [math] v [/math] и вершинами компоненты связности графа [math] G' - v [/math], содержащей [math] a [/math], а через [math] G'_2 [/math] - подграф графа [math] G' [/math], порождённый вершиной [math] v [/math] и вершинами остальных компонент связности графа [math] G' - v [/math] (в этом множестве лежит вершина [math] b [/math]). Пусть [math] G''_1 = G'_1 + e_1 [/math], где [math] e1 = vb [/math] - новое ребро (рис. 4) рис. 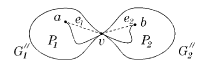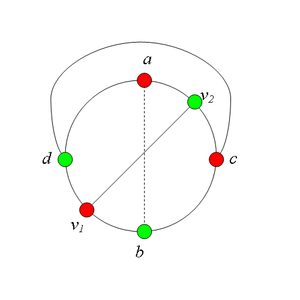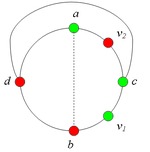4 Заметим, что в графе [math] G''_1 [/math] рёбер меньше, чем в графе [math] G [/math]. Действительно, вместо ребра [math] e [/math] в [math] G''_1 [/math] есть ребро [math] e1 [/math] и часть рёбер из графа [math] G [/math] осталась в графе [math] G''_2 [/math]. Аналогично, в графе [math] G''_2 [/math] рёбер меньше, чем в графе [math] G [/math]. Покажем, далее, что в графе [math] G''_1 [/math] и, аналогично, в графе [math] G''_2 [/math] нет подграфов, гомеоморфных [math] K_5 [/math] или [math] K_{3,3} [/math]. Действительно, если в [math] G''_1 [/math] имеется такой подграф, то в этом подграфе присутствует вновь присоединенное ребро, но это ребро [math] e1 [/math] можно заменить на цепь a -> b -> ... -> v, взяв некоторую простую (b, v)-цепь [math] P_2 [/math] в графе [math] G'_2 [/math]. Следовательно, мы получили подграф в [math] G [/math], гомеоморфный [math] К_5 [/math] или [math] К_{3,3} [/math], что невозможно. Теперь в силу минимальности графа [math] G [/math] графы [math] G''_1 [/math] и [math] G''_2 [/math] планарны. Возьмем укладку графа [math] G''_1 [/math] на плоскости такую, что ребро [math] е1 = av [/math] лежит на границе внешней грани. Во внешней грани графа [math] G''_1 [/math] возьмем укладку графа [math] G''_2 [/math] такую, что ребро [math] е2 = vb [/math] лежит па границе внешпей грани (рис. 5). рис. 5 Отметим, что опять вершина [math] v [/math] представлена на плоскости в двух экземплярах. Очевидно, добавление ребра [math] е = ab [/math] не меняет планарности графа [math] G''_1 U G''_2[/math]. Склеим оба вхождения вершины [math] v [/math] точно так же, как это мы сделали в предыдущем пункте доказательства (рис. 6). рис. 6 Сотрем затем ранее добавленные ребра [math] е1 [/math] и [math] е2 [/math]. В результате мы получим укладку графа [math] G [/math] на плоскости, что невозможно. Утверждение доказано. Среди всех укладок графа [math]G'[/math] на плоскости и среди всех циклов [math]C[/math], содержащих [math]a[/math] и [math]b[/math], зафиксируем такую укладку и такой цикл, что внутри области, ограниченной циклом [math]C[/math], лежит максимальное возможное число граней графа [math]G'[/math]. Зафиксируем один из обходов по циклу [math]C[/math] (на рисунках будем рассматривать обход по часовой стрелке по циклу [math]C[/math]). Для вершин [math]u[/math] и [math]v[/math] цикла [math]C[/math] через [math]C[u,v][/math] будем обозначать простую [math](u,v)[/math]-цепь, идущую по циклу [math]C[/math] от [math]u[/math] до [math]v[/math] в направлении обхода цикла. Конечно, [math]C[u,v] ≠ C[v,u][/math]. Положим [math]C(u,v) = C[u,v] \ {u,v}[/math], т.е. [math]C(u,v)[/math] получено из [math]C[u,v][/math] отбрасыванием вершин [math]u[/math] и [math]v[/math]. Определение: Внешним графом (относительно цикла [math]C[/math]) будем называть подграф графа [math]G'[/math], порождённый всеми вершинами графа [math]G'[/math], лежащими снаружи от цикла [math]C[/math]. Определение: Внешними компонентами будем называть компоненты связности внешнего графа. В силу связности графа [math]G'[/math] для любой внешней компоненты должны существовать рёбра в [math]G'[/math], соединяющие её с вершинами цикла [math]C[/math]. Определение: Внешними частями будем называть: a) внешние компоненты вместе со всеми рёбрами, соединяющими компоненту с вершинами цикла [math]C[/math], и инцидентными им вершинами; б) рёбра графа [math]G'[/math], лежащие снаружи от цикла [math]C[/math] и соединяющие две вершины из [math]C[/math], вместе с инцидентными такому ребру вершинами. Определение: Внутренним графом (относительно цикла [math]C[/math]) будем называть подграф графа [math]G'[/math], порождённый всеми вершинами графа [math]G'[/math], лежащими внутри цикла [math]C[/math]. Определение: Внутренними компонентами будем называть компоненты связности внутреннего графа. В силу связности графа [math]G'[/math] для любой внутренней компоненты должны существовать рёбра в [math]G'[/math], соединяющие её с вершинами цикла [math]C[/math]. Определение: Внутренними частями будем называть: a) внутренние компоненты вместе со всеми рёбрами, соединяющими компоненту с вершинами цикла [math]C[/math], и инцидентными им вершинами; б) рёбра графа [math]G'[/math], лежащие внутри цикла [math]C[/math] и соединяющие две вершины из [math]C[/math], вместе с инцидентными такому ребру вершинами. Будем говорить, что внешняя (внутренняя) часть встречает цикл [math]C[/math] в своих точках прикрепления к циклу [math]C[/math]. Шаблон:Утверждение 5 Определение: Ввиду утверждения 5 будем говорить, что любая внешняя часть является [math](a,b)[/math]-разделяющей частью, поскольку она встречает и [math]C(a,b)[/math], и [math]C(b,a)[/math]. 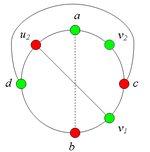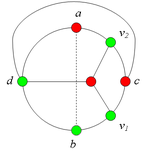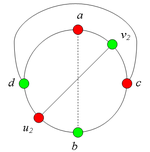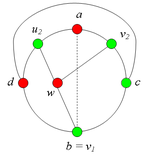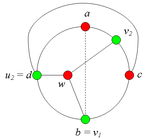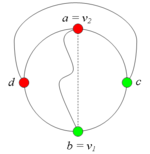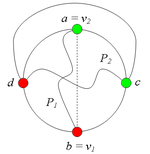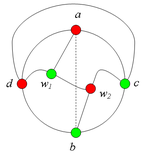Аналогично можно ввести понятие [math](a,b)[/math]-разделяющей внутренней части. Заметим, что внутрення часть может встречать цикл [math]C[/math], вообще говоря, более чем в двух точках, но не менее чем в двух точках. Шаблон:Утверждение 6 Шаблон:Утверждение 7 Разбор случаев взаимного положения a, b, c, d, u1, u2, v1, v2 Рассмотрим 2 случая. рис. 1 1. Пусть пара вершин [math]\ v_1 [/math] и [math]\ v_2 [/math] является [math](a, b)[/math]-разделяющей. Тогда, в частности, [math]v_2 \ne a[/math] и [math] v_1 \ne b[/math]. В этом случае граф G содержит подграф, гомеоморфный [math]\ K_{3,3} [/math] (отметим, что в [math] In [/math] существует простая [math](v_1, v_2)[/math]-цепь)(рис. 1). 2. Пусть пара вершин [math]v_1[/math] и [math]v_2[/math] не является [math](a, b)[/math]-разделяющей. Тогда [math]v_1, v_2[/math] лежат на [math]C[a, b][/math] или на [math]C[b, a][/math]. Без ограничения общности будет считать, что [math]v_1[/math] и [math]v_2[/math] лежат на [math]C[a, b][/math]. 2.1. Пусть [math]v_1[/math] и [math]v_2[/math] лежат на [math]C(a, b)[/math], т.е. [math]v_1 \ne b[/math] и [math]v_2 \ne a[/math](рис. 2). 2.1.1 Пусть [math]u_2[/math] лежит на [math]C(d, a)[/math]. Тогда в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math](рис. 3). 2.1.2. Пусть [math]u_2 = d[/math]. Тогда во внешней части [math]In[/math] имеется вершина [math]w[/math] и три простые цепи от [math]w[/math] соответственно до [math]d, v_1, v_2[/math], которые в качестве общей точки имеют только точку [math]w[/math]. В этом случае в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math](рис. 4). 2.1.3. Пусть [math]u_2[/math] лежит на [math]C(b, d)[/math]. Тогда в графе G есть подграф, гомеоморфный [math]K{3,3}[/math](рис. 5). Теперь рассмотрим случаи, когда хотя бы одна из вершин [math]v_1[/math] и [math]v_2[/math] не лежит на [math]С(a, b)[/math]. Без ограничения общности будем считать, что это вершина [math]v_1[/math], т.е [math]v_1 = b[/math](поскольку [math]v_1[/math] лежит на [math]C[a, b][/math]). 2.2. Пусть [math]v_2 \ne a[/math]. 2.2.1. Пусть [math]u_2[/math] лежит на [math]C(d, a)[/math]. Тогда в графе G есть пограф, гомеоморфный [math]K_{3,3}[/math](рис. 6). 2.2.2. Пусть [math]u_2 = d[/math]. Тогда в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math](рис. 7). 2.2.3. Пусть [math]u_2[/math] лежит на [math]C(b, d)[/math]. Тогда в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math](рис. 8). 2.3. Пусть [math]v_2 = a[/math](рис. 9). Рассмотрим теперь пару вершин [math]u_1[/math] и [math]u_2[/math]. Будем считать, что [math]u_1 = c[/math] и [math]u_2 = d[/math], поскольку все другие случаи расположения вершин [math]u_1[/math] и [math]u_2[/math] так же, как были рассмотрены все случаи расположения [math]v_1[/math] и [math]v_2[/math]. Пусть [math]P_1[/math] и [math]P_2[/math] -- соответственно кратчайшие простые [math](a, b)[/math]-цепь и [math](c, d)[/math]-цепь по внутренней части [math]In[/math](рис. 10). Заметим, что [math]P_1[/math] и [math]P_2[/math] имеют общую точку. 2.3.1. Пусть цепи [math]P_1[/math] и [math]P_2[/math] имеют более одной общей точки. Тогда в графе G есть подграф, гомеоморфный [math]K_{3,3}[/math](рис. 11). 2.3.2. Пусть цепи [math]P_1[/math] и [math]P_2[/math] имеют точно одну общую точку [math]w[/math]. Тогда в графе G есть подграф, гомеоморфный [math]K_5[/math](рис. 12). Таким образом, доказано, что в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math] или [math]K_5[/math], что противоречит нашему первому предположению.

[math]\triangleleft[/math]

Литература

• Асанов М,, Баранский В., Расин В. - Дискретная математика - Графы, матроиды, алгоритмы