Интерполяционный поиск — различия между версиями
| Строка 33: | Строка 33: | ||
== Время работы == | == Время работы == | ||
| − | |||
Асимптотически интерполяционный поиск превосходит по своим характеристикам бинарный. Если ключи распределены случайным образом, то за один шаг алгоритм уменьшает количество проверяемых элементов с <tex> n </tex> до <tex> \sqrt n </tex> | Асимптотически интерполяционный поиск превосходит по своим характеристикам бинарный. Если ключи распределены случайным образом, то за один шаг алгоритм уменьшает количество проверяемых элементов с <tex> n </tex> до <tex> \sqrt n </tex> | ||
<ref>[http://www.cs.technion.ac.il/~itai/publications/Algorithms/p550-perl.pdf Interpolation Search {{---}} A LogLogN Search]</ref>. То есть, после <tex>k</tex>-ого шага количество проверяемых элементов уменьшается до <tex dpi = 170>n^{\frac{1}{2^k}}</tex>. Значит, остаётся проверить только 2 элемента (и закончить на этом поиск), когда <tex dpi = 150>\frac{1}{2^k} = \log_{n}2 = \frac{1}{\log_{2}n} </tex>. Из этого вытекает, что количество шагов, а значит, и время работы составляет <tex>O(\log \log n)</tex>. | <ref>[http://www.cs.technion.ac.il/~itai/publications/Algorithms/p550-perl.pdf Interpolation Search {{---}} A LogLogN Search]</ref>. То есть, после <tex>k</tex>-ого шага количество проверяемых элементов уменьшается до <tex dpi = 170>n^{\frac{1}{2^k}}</tex>. Значит, остаётся проверить только 2 элемента (и закончить на этом поиск), когда <tex dpi = 150>\frac{1}{2^k} = \log_{n}2 = \frac{1}{\log_{2}n} </tex>. Из этого вытекает, что количество шагов, а значит, и время работы составляет <tex>O(\log \log n)</tex>. | ||
| Строка 40: | Строка 39: | ||
Эксперименты показали, что интерполяционный поиск не настолько снижает количество выполняемых сравнений, чтобы компенсировать требуемое для дополнительных вычислений время (пока таблица не очень велика). Кроме того, типичные таблицы недостаточно случайны, да и разница между значениями <tex>\log \log n</tex> и <tex>\log n</tex> становится значительной только при очень больших <tex>n</tex>. На практике при поиске в больших файлах оказывается выгодным на ранних стадиях применять интерполяционный поиск, а затем, когда диапазон существенно уменьшится, переходить к двоичному. | Эксперименты показали, что интерполяционный поиск не настолько снижает количество выполняемых сравнений, чтобы компенсировать требуемое для дополнительных вычислений время (пока таблица не очень велика). Кроме того, типичные таблицы недостаточно случайны, да и разница между значениями <tex>\log \log n</tex> и <tex>\log n</tex> становится значительной только при очень больших <tex>n</tex>. На практике при поиске в больших файлах оказывается выгодным на ранних стадиях применять интерполяционный поиск, а затем, когда диапазон существенно уменьшится, переходить к двоичному. | ||
| + | |||
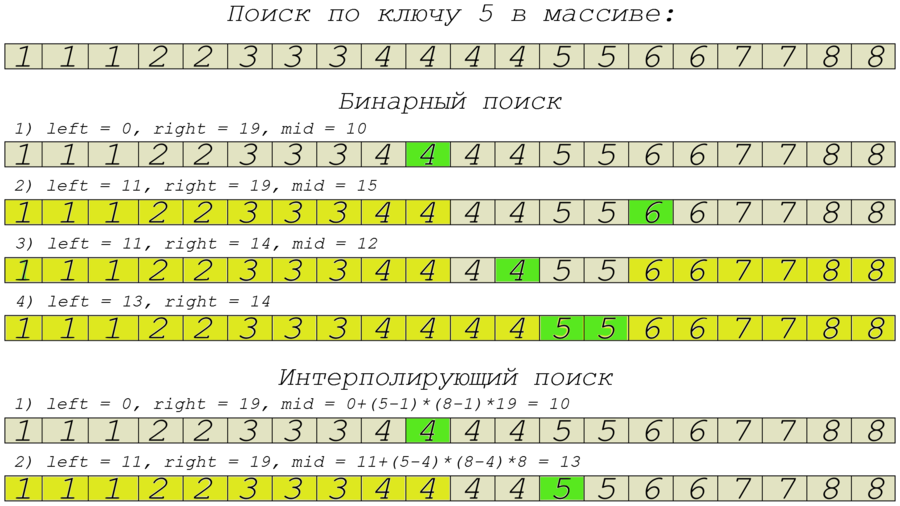
| + | ===Пример работы вместе с сравнением с бинарным поиском=== | ||
| + | [[Файл:ip_vs_bin_from_gshark.png|900px|center|Сравнение бинарного и интерполирующего поисков]] | ||
==Примечания== | ==Примечания== | ||
Версия 22:58, 15 июня 2014
Содержание
Идея
Рассмотрим задачу: найти слово в словаре. Если оно начинается на букву "А", то никто не будет искать его в середине, а откроет словарь ближе к началу. В чём разница между алгоритмом человека и другими? Отличие заключается в том, что алгоритмы вроде двоичного поиска не делают различий между "немного больше" и "существенно больше".
Алгоритм
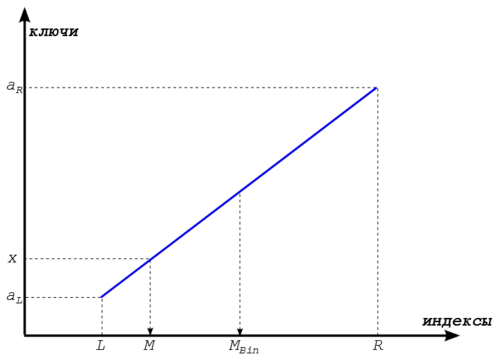
Пусть — отсортированный массив из чисел, — значение, которое нужно найти. Поиск происходит подобно двоичному поиску, но вместо деления области поиска на две примерно равные части, интерполирующий поиск производит оценку новой области поиска по расстоянию между ключом и текущим значением элемента. Если известно, что лежит между и , то следующая проверка выполняется примерно на расстоянии от .
Формула для разделительного элемента получается из следующего уравнения: — откуда следует, что . На рисунке внизу показано, из каких соображений берется такая оценка. Интерполяционный поиск основывается на том, что наш массив представляет из себя что-то наподобии арифметической прогрессии.
Псевдокод
int interpolationSearch(a : int[], key : int) // a должен быть отсортирован
left = 0 // левая граница поиска (будем считать, что элементы массива нумеруются с нуля)
right = a.length - 1 // правая граница поиска
while a[left] < key and key < a[right]
mid = left + (key - a[left]) * (right - left) / (a[right] - a[left]) // индекс элемента, с которым будем проводить сравнение
if a[mid] < key
left = mid + 1
else if a[mid] > key
right = mid - 1
else
return mid
if a[left] == key
return left
else if a[right] == key
return right
else
return -1 // если такого элемента в массиве нет
Время работы
Асимптотически интерполяционный поиск превосходит по своим характеристикам бинарный. Если ключи распределены случайным образом, то за один шаг алгоритм уменьшает количество проверяемых элементов с до [1]. То есть, после -ого шага количество проверяемых элементов уменьшается до . Значит, остаётся проверить только 2 элемента (и закончить на этом поиск), когда . Из этого вытекает, что количество шагов, а значит, и время работы составляет .
При "плохих" исходных данных (например, при экспоненциальном возрастании элементов) время работы может ухудшиться до .
Эксперименты показали, что интерполяционный поиск не настолько снижает количество выполняемых сравнений, чтобы компенсировать требуемое для дополнительных вычислений время (пока таблица не очень велика). Кроме того, типичные таблицы недостаточно случайны, да и разница между значениями и становится значительной только при очень больших . На практике при поиске в больших файлах оказывается выгодным на ранних стадиях применять интерполяционный поиск, а затем, когда диапазон существенно уменьшится, переходить к двоичному.
Пример работы вместе с сравнением с бинарным поиском
Примечания
Источники информации
- Дональд Кнут — Искусство программирования. Том 3. Сортировка и поиск. / Knuth D.E. — The Art of Computer Programming. Vol. 3. Sorting and Searching.
- Wikipedia — Interpolation search
- Википедия — Интерполирующий поиск