Моноид — различия между версиями
Shersh (обсуждение | вклад) м |
Shersh (обсуждение | вклад) (конспект структурирован) |
||
| Строка 9: | Строка 9: | ||
Другими словами, моноид {{---}} это [[Полугруппа|полугруппа]], в которую добавлен нейтральный элемент. | Другими словами, моноид {{---}} это [[Полугруппа|полугруппа]], в которую добавлен нейтральный элемент. | ||
| − | Примеры | + | == Примеры == |
* множество натуральных чисел <tex> \mathbb{N} </tex> с операцией сложения является моноидом <tex>\langle \mathbb{N}, +, 0 \rangle</tex> | * множество натуральных чисел <tex> \mathbb{N} </tex> с операцией сложения является моноидом <tex>\langle \mathbb{N}, +, 0 \rangle</tex> | ||
* множество положительных целых <tex> \mathbb{Z}_+ </tex> с операцией умножения является моноидом <tex>\langle\mathbb{Z}_+, \cdot, 1 \rangle</tex> | * множество положительных целых <tex> \mathbb{Z}_+ </tex> с операцией умножения является моноидом <tex>\langle\mathbb{Z}_+, \cdot, 1 \rangle</tex> | ||
* множество натуральных числел '''не''' является моноидом по умножению с нейтральным элементом <tex>1</tex>, так как <tex>1 \cdot 0 = 0</tex>, а не <tex>1</tex>, как того требует аксиома нейтрального элемента. | * множество натуральных числел '''не''' является моноидом по умножению с нейтральным элементом <tex>1</tex>, так как <tex>1 \cdot 0 = 0</tex>, а не <tex>1</tex>, как того требует аксиома нейтрального элемента. | ||
| + | |||
| + | == Свойства == | ||
{{Утверждение | {{Утверждение | ||
| Строка 22: | Строка 24: | ||
}} | }} | ||
| + | == Гомоморфизм моноидов == | ||
{{Определение | {{Определение | ||
|id = defmonhom | |id = defmonhom | ||
| Строка 30: | Строка 33: | ||
* <tex> \forall x, y \in M \colon \varphi(x\cdot_M y) = \varphi(x) \cdot_N \varphi(y)</tex> | * <tex> \forall x, y \in M \colon \varphi(x\cdot_M y) = \varphi(x) \cdot_N \varphi(y)</tex> | ||
}} | }} | ||
| + | |||
| + | == Свободный моноид над множеством == | ||
{{Определение | {{Определение | ||
| Строка 35: | Строка 40: | ||
'''Свободным моноидом''' (англ. ''free monoid'') <tex> M </tex> '''над множеством''' <tex> S </tex> <tex>(</tex>обозначается как <tex> M_S )</tex> называется моноид над множеством <tex> S^* </tex> {{---}} набором всевозможных последовательностей (или списков) конечной длины (в том числе и нулевой), образованных из элементов множества <tex> S </tex> {{---}} с ассоциативной операцией [[Основные определения: алфавит, слово, язык, конкатенация, свободный моноид слов; операции над языками#defconcat|конкатенации]] <tex>\texttt{++}</tex> этих последовательностей. | '''Свободным моноидом''' (англ. ''free monoid'') <tex> M </tex> '''над множеством''' <tex> S </tex> <tex>(</tex>обозначается как <tex> M_S )</tex> называется моноид над множеством <tex> S^* </tex> {{---}} набором всевозможных последовательностей (или списков) конечной длины (в том числе и нулевой), образованных из элементов множества <tex> S </tex> {{---}} с ассоциативной операцией [[Основные определения: алфавит, слово, язык, конкатенация, свободный моноид слов; операции над языками#defconcat|конкатенации]] <tex>\texttt{++}</tex> этих последовательностей. | ||
}} | }} | ||
| + | === Примеры свободного моноида над множеством === | ||
* тривиальный пример: множество <tex> S = \varnothing </tex>. Тогда <tex> S^* = \{\varnothing\} </tex>. | * тривиальный пример: множество <tex> S = \varnothing </tex>. Тогда <tex> S^* = \{\varnothing\} </tex>. | ||
* <tex> S = \{1\} </tex>. Тогда <tex>S^* = \{[], [1], [1, 1], ... \} </tex>. | * <tex> S = \{1\} </tex>. Тогда <tex>S^* = \{[], [1], [1, 1], ... \} </tex>. | ||
| + | |||
| + | == Свободный моноид == | ||
{{Определение | {{Определение | ||
| Строка 43: | Строка 51: | ||
Моноид <tex>M</tex> называется '''свободным''', если он [[Изоморфизм групп | изоморфен]] некоторому свободному моноиду над каким-то множеством. | Моноид <tex>M</tex> называется '''свободным''', если он [[Изоморфизм групп | изоморфен]] некоторому свободному моноиду над каким-то множеством. | ||
}} | }} | ||
| + | === Примеры свободного моноида === | ||
* <tex>\langle \mathbb{N}, +, 0 \rangle </tex> {{---}} пример свободного моноида, так как он изоморфен свободному моноиду над <tex>S = \{1\}</tex>: | * <tex>\langle \mathbb{N}, +, 0 \rangle </tex> {{---}} пример свободного моноида, так как он изоморфен свободному моноиду над <tex>S = \{1\}</tex>: | ||
| Строка 48: | Строка 57: | ||
** <tex>i(a + b) = i(a) ~ \texttt{++} ~ i(b)</tex> | ** <tex>i(a + b) = i(a) ~ \texttt{++} ~ i(b)</tex> | ||
| + | == Моноид с порождающими соотношениями == | ||
Введём дополнительное определение, чтобы привести пример моноида, не являющегося свободным. | Введём дополнительное определение, чтобы привести пример моноида, не являющегося свободным. | ||
Версия 01:53, 18 ноября 2013
| Определение: |
Кортеж называется моноидом, если он удовлетворяет следующим аксиомам:
|
Другими словами, моноид — это полугруппа, в которую добавлен нейтральный элемент.
Содержание
Примеры
- множество натуральных чисел с операцией сложения является моноидом
- множество положительных целых с операцией умножения является моноидом
- множество натуральных числел не является моноидом по умножению с нейтральным элементом , так как , а не , как того требует аксиома нейтрального элемента.
Свойства
| Утверждение (О единственности нейтрального элемента): |
Нейтральный элемент в моноиде единственен. |
| Действительно, пусть и — два нейтральных элемента. Тогда имеем: . |
Гомоморфизм моноидов
| Определение: |
| Гомоморфизмом моноидов (англ. monoid homomorphism) и называется отображение совместимое с операциями из и , то есть такое, что:
|
Свободный моноид над множеством
| Определение: |
| Свободным моноидом (англ. free monoid) над множеством обозначается как называется моноид над множеством — набором всевозможных последовательностей (или списков) конечной длины (в том числе и нулевой), образованных из элементов множества — с ассоциативной операцией конкатенации этих последовательностей. |
Примеры свободного моноида над множеством
- тривиальный пример: множество . Тогда .
- . Тогда .
Свободный моноид
| Определение: |
| Моноид называется свободным, если он изоморфен некоторому свободному моноиду над каким-то множеством. |
Примеры свободного моноида
- — пример свободного моноида, так как он изоморфен свободному моноиду над :
Моноид с порождающими соотношениями
Введём дополнительное определение, чтобы привести пример моноида, не являющегося свободным.
| Определение: |
| Моноидом с порождающими отношениями (англ. equational presentation of monoid) называется моноид, на котором введены дополнительные правила (то есть бинарные отношения на строках), отождествляющие некоторые элементы моноида. |
Примером такого моноида является множество всевозможных строк над алфавитом , , что обозначает равенство строк и в моноиде. И хотя такой моноид образован всевозможными последовательностями, он не является свободным. Покажем это.
| Теорема: |
Моноид не является свободным |
| Доказательство: |
|
Для начала покажем, что каждый элемент такого моноида можно представить в виде . Докажем это конструктивно. Возьмём произвольную строку и будем в ней заменять все подстроки вида на подстроки . Если таких подстрок нет, то наша строка имеет вид , а если есть, то строка за конечное число шагов приведётся к указанному виду, потому что операцию замены на можно рассматривать, как уменьшения числа инверсий в последовательности, а их точно конечное число, так как все последовательности имеют конечную длину. Замечание: конкатенация двух последовательностей и аналогична операции конкатенации строк, только после её применения строку надо привести к виду , поэтому результат операции равен не конкретной строке, а целому классу эквивалентности. Предположим, что данный моноид свободный. Это значит, что он изоморфен какому-то свободному моноиду над множество , то есть существует биективное отображение . Оно сохраняет ассоциативность операций, поэтому
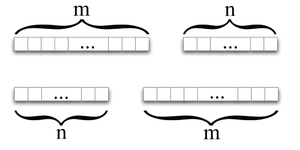
Следовательно, так как и отображение является изоморфизмом, то . Пусть . Равенство этих последовательностей означает, что у последовательности есть два бордера длин и соответственно, значит, она периодическая и имеет период равный НОД. Из этого следует, что последовательности и можно представить в виде конечного объединения некоторой подпоследовательности , являющейся периодом и имеющей длину НОД.
Пусть НОК, тогда
Откуда следует, что , то есть отображение не является изоморфизмом. Значит, мы пришли к противоречию, предположив, что данный моноид является свободным. Равенство может сохранять изоморфизм, если , но тогда , что опять же приводит нас к противоречию. |