Алгоритм "Вперед-Назад"

Пусть дана скрытая Марковская модель [math]\lambda = \{S, \Omega, \Pi, A, B\}[/math], где [math]S = \{s_1, ..., s_n\}[/math] — состояния, [math]\Omega = \{\omega_1, ..., \omega_m\}[/math] — возможные события, [math]\Pi = \{\pi_1, ..., \pi_n\}[/math] — начальные вероятности, [math]A = \{a_{ij}\}[/math] — матрица переходов, а [math]B = \{b_{i\omega_k}\}[/math] — вероятность наблюдения события [math]\omega_k[/math] после перехода в состояние [math]s_i[/math].

За [math]T[/math] шагов в этой модели получилась последовательность наблюдений [math]O_{1,T} = {o_1, ..., o_T}[/math].

Алгоритм "вперед-назад" позволяет найти в скрытой Марковской модели вероятность попадания в состояние [math]s_i[/math] на [math]t[/math]-ом шаге при последовательности наблюдений [math]O[/math] и (скрытой) последовательности состояний [math]X[/math].

Вычисление

Пусть в момент [math]t[/math] мы оказались в состоянии [math]i[/math]: [math]X_t = i[/math]. Назовем [math]\alpha_{i}(t)[/math] вероятность того, что при этом во время переходов образовалась последовательность наблюдений [math]O_{1,t-1}[/math], а [math]\beta_{i}(t)[/math] — вероятность того, что после этого состояния мы будем наблюдать последовательность наблюдений [math]O_{t,T}[/math]:

[math]\alpha_{i}(t) \overset{def}{=} P(O_{1, t-1} | X_t = i) \\ \beta_i(t) \overset{def}{=} P(O_{t,T} | X_t = i)[/math]

Нам требуется найти [math]P(X_t = i | O) = P(X_t = i | O_{1,t-1} \cap O_{t,T})[/math]. Поскольку будущее Марковской цепи не зависит от прошлого, мы можем утверждать, что вероятность того, что мы будем наблюдать события [math]O_{t,T}[/math] не зависит от того, что в прошлом мы наблюдали последовательность [math]O_{1,t-1}[/math], и, следовательно:

[math]P(X_t = i | O_{1,t-1} \cap O_{t,T}) =[/math] [math]\frac{P(X_t = i | O_{1,t-1}) \cdot P(X_t = i | O_{t,T})}{P(O)}[/math] [math]=[/math] [math]\frac{\alpha_{i}(t) \cdot \beta_{i}(t)}{P(O)}[/math]

Проход вперед

Заметим, что в [math]\{\alpha_s(1)\}[/math] нужно считать равной [math]\pi_s b_{so_1}[/math], как вероятность получить первое событие из начального распределения.

Для следующих [math]t[/math] можно вычислить [math]\alpha_s(t)[/math] рекуррентно:

[math]\alpha_{s}(t) = P(O_{1, t} | X_t = s_i) = \\ = \displaystyle\sum\limits_{j \in S} P(O_{1, t} | X_t = s \cap X_{t-1} = j) = \\ = \displaystyle\sum\limits_{j \in S} P(O_{1, t-1} | X_{t-1} = j) \cdot P(X_t = s | X_{t-1} = j) \cdot P(O_t = o_t | X_t = s) = \\ = \displaystyle\sum\limits_{j \in S} \alpha_{j}(t-1) \cdot a_{js} \cdot b_{so_t} = \\ = b_{so_t} \cdot \displaystyle\sum\limits_{j \in S} \alpha_{j}(t-1) \cdot a_{js}[/math]

Итак, вероятность попасть в состояние [math]s[/math] на [math]t[/math]-ом шаге, учитывая, что после перехода произойдет событие [math]o_t[/math] будет равна вероятности быть в состоянии [math]j[/math] на [math]t[/math]-ом шаге, умноженной на вероятность перейти из состояния [math]j[/math] в [math]s[/math], произведя событие [math]o_t[/math] для всех [math]j \in S[/math].

Проход назад

Аналогично, [math]\beta_s(T+1) = 1[/math], так как произвольная цепочка наблюдений будет произведена, какими бы ни были состояния.

Предыдущие [math]\beta_s(t)[/math] считаются рекуррентно:

[math]\beta_s(t) = P(O_{t, T} | X_t = s) = \\ = \displaystyle\sum\limits_{j \in S} P(O_{t+1,T} | X_{t+1} = j) \cdot P(X_{t+1} = j | X_t = s) \cdot P(o_{t+1} | X_t = s) = \\ = \displaystyle\sum\limits_{j \in S} \beta_j(t+1) \cdot a_{sj} \cdot b_{jo_{t+1}}[/math]

Сглаживание вероятности

Итак, для произвольного состояния [math]s[/math] в произвольный шаг [math]t[/math] теперь известна вероятность того, что на пути к нему была произведена последовательность [math]O_{1,t}[/math] и вероятность того, что после него будет произведена последовательность [math]O_{t+1,T}[/math]. Чтобы найти вероятность того, что будет произведена цепочка событий, найти [math]P(O)[/math], нужно просуммировать произведение обеих вероятностей для всех состояний при произвольном шаге t: [math]P(O) = \sum_{s \in S} \alpha_s(t)\beta_s(t)[/math].

Теперь найдем вероятность того, что в момент [math]t[/math] цепь будет в состоянии [math]s[/math]:

[math]P(X_t = s | O) = P(X_t = s | O_{1,t-1} \cap O_{t,T}) =[/math] [math]\frac{P(X_t = s | O_{1,t-1}) \cdot P(X_t = s | O_{t,T})}{P(O)}[/math] [math]=[/math] [math]\frac{\alpha_{s}(t) \cdot \beta_{s}(t)}{P(O)}[/math] [math]=[/math]

[math]=[/math] [math]\frac{\alpha_s(t)\cdot \beta_s(t)}{\sum_{i \in S}\alpha_s(t)\cdot \beta_s(t)}[/math]

Пример

Пример СММ

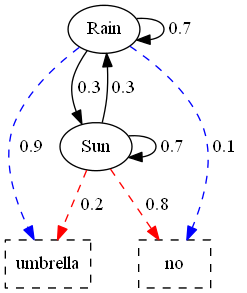
Пусть ваша жизнь не удалась и вам пришлось работать охранником в холле офисного здания. Каждое утро вы наблюдали за тем, как один и тот же мужчина либо приносил, либо не приносил зонтик в зависимости от погоды. Увлекаясь статистикой, вы выяснили, что за день погода может поменяться с вероятностью [math]0.3[/math]; если на улице идет дождь, то мужчина приносит зонтик с вероятностью [math]0.9[/math], а если солнечно — то с вероятностью [math]0.2[/math] (пример справа).

Но вот вас переводят смотреть за камерами наблюдения: теперь вы не можете наблюдать за погодой, но каждый день видите того мужчину. За рабочую неделю вы заметили, что он не принес зонтик лишь в среду. С какой вероятностью во вторник шел дождь?

По вышесказанному, [math]P(X_2 = Rain | \{umbrella, umbrella, no, umbrella, umbrella\}) =[/math] [math]\frac{\alpha_{Rain}(2)\cdot \beta_{Rain}(2)}{\sum_{i \in \{Rain, Sun\}}\alpha_i(2)\cdot \beta_i(2)}[/math] [math]=[/math] [math]\frac{\alpha_{Rain}(2)\cdot \beta_{Rain}(2)}{\alpha_{Rain}(2)\cdot \beta_{Rain}(2) + \alpha_{Sun}(2)\cdot \beta_{Sun}(2)}[/math] [math]\approx 0.820[/math].

Итак, с вероятностью [math]\approx 82\%[/math] во вторник шел дождь.

Псевдокод

 /* fwd, bkw -- матрицы размера |S|*T, которым во время работы присваиваются промежуточные результаты alpha и beta */
    
 for s in S
     fwd[s, 1] = emit_probability[s][observations[1]] * П[s]
     bkw[s, len(observations) - 1] = 1
 
 function alpha(s, t)
     if (s, t) in fwd:
         return fwd[s, t]
      
     f = 0
     for j in S:
         f += alpha(j, t-1) * transition_probability[j][s]
     
     f *= emit_probability[s][observations[t]]
     fwd[s, t] = f
     return fwd[s, t]
     
 function beta(s, t)
     if (s, t) in bkw
         return bkw[s, t]
     b = 0
     for j in S:
         b += beta(j, t+1) * transition_probability[s][j] * emit_probability[j][O[t+1]]
     
     bkw[s, t] = b
     return bkw[s, t]
     
 function forward_backward()
     probabilities = {}
     chain_probability = 0
     for j in S:
         chain_probability += alpha(j, t)*beta(j, t)
      
     for s in S
         for t in [1, T]
             probabilities[s, t] = (alpha(s, t) * beta(s, t)) / chain_probability

     return probabilities