| Имя входного файла: | input.txt |
| Имя выходного файла: | output.txt |
| Ограничение по времени: | 5 секунд |
| Максимальная оценка: | 25 баллов |
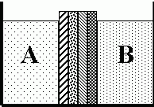
Для хранения двух агрессивных жидкостей A и B используется емкость с многослойной перегородкой, которая изготавливается из имеющихся N листов. Для каждого листа i (i = 1, ..., N) известно время его растворения жидкостью A - ai и жидкостью B - bi. Растворение перегородки каждой из жидкостей происходит последовательно лист за листом, с постоянной скоростью по толщине листа. Требуется спроектировать такую перегородку, время растворения которой было бы максимальным.

В первой строке входного файла записано число N (1 ≤ N ≤ 256). В каждой из последующих N строк содержатся два положительных вещественных числа ai и bi, разделенные пробелом.
В первую строку выходного файла записать время растворения перегородки с точностью до 3 цифр после десятичной точки. В следующую строку файла записать номера листов в порядке их расположения от жидкости A к жидкости B, разделяя числа пробелами.
| input.txt | output.txt |
4 1 2 1 2 0.5 1.5 7 3.5 | 6.000 4 2 1 3 |
| Имя входного файла: | input.txt |
| Имя выходного файла: | output.txt |
| Ограничение по времени: | 10 секунд |
| Максимальная оценка: | 35 баллов |
Для того, чтобы выдержать собеседование при приеме на работу в качестве программиста в некоторую компьютерную фирму, претендент должен уметь решать задачи по следующим четырем темам: динамическое программирование, перебор с возвратом, теория графов и вычислительная геометрия. Полностью подготовиться к тестовому собеседованию можно, решая задачи из пособия, изданного этой фирмой.
Уровень подготовки программиста по каждой из перечисленных тем оценивается своим индексом UP по L-балльной шкале от 1 до L. Для каждой из задач определены минимальные UP программиста по каждой из тем, необходимые для того, чтобы он смог решить данную задачу. Определены также UP, которых программист достигнет, решив ее. Если при этом по какой-то из тем он уже имел более высокий UP, то этот уровень не понизится. На решение задачи, повышающей хотя бы один из UP, программист тратит 2 часа, в противном случае - 1 час.
Требуется разработать учебный план, занимаясь по которому не более T часов, начинающий программист (UP=1 по всем темам) достиг бы уровня подготовки L по всем темам, прорешав за это время как можно больше различных задач.
В первой строке входного файла задано число T - количество часов, которыми располагает претендент для подготовки к собеседованию. Во второй строке записано число L (2 ≤ L ≤ 16), а в третьей строке - количество задач M (1 ≤ M ≤ 500, 2 ≤ T ≤ M). Каждая из последующих M строк содержит 8 чисел, описывающих одну из задач. Первые четыре числа определяют UP претендента по всем темам, необходимые для того, чтобы он мог решить эту задачу. Следующие четыре числа задают UP, до которых в результате решения этой задачи повысятся те уровни подготовки претендента, которые были ниже.
При возможности достижения уровня подготовки L по всем темам в выходной файл вывести сначала максимальное количество задач в учебном плане, а затем - последовательность номеров задач, которые должен решить претендент. Задачи нумеруются в том порядке, в каком они описаны во входном файле, ни одна задача не может быть указана более одного раза. Если с помощью указанного во входном файле набора задач за время T начинающий программист не сможет достигнуть UP, равного L по всем темам, вывести в выходной файл одно число 0.
| input.txt | output.txt |
7 5 6 2 1 1 1 2 4 5 5 1 1 1 1 3 1 1 1 3 3 3 3 3 3 3 3 1 3 1 1 5 5 5 5 2 2 2 2 2 2 2 2 1 2 3 4 2 3 4 5 | 4 2 1 4 3 |
| Имя входного файла: | input.txt |
| Имя выходного файла: | output.txt |
| Ограничение по времени: | 10 секунд |
| Максимальная оценка: | 40 баллов |
Царство царя Гороха представляет собой выпуклый N-угольник, внутри которого расположены K селений. Царь решил завещать двум своим сыновьям по полцарства, одинаковые по площади и с равным количеством селений. Для этого он требует разделить царство одной прямолинейной границей.
Напишите программу, строящую границу согласно царской воле. Если граница проходит через селение, то оно может быть либо отнесено к одному из полуцарств, либо разделено на два селения, которые будут отнесены к разным полуцарствам (при нечетном K граница, естественно, должна разделить какое-то из селений).
Первая строка входного файла содержит количество вершин многоугольника N (3 ≤ N ≤ 50). В следующих N строках заданы координаты вершин многоугольника, перечисленные в порядке обхода контура по часовой стрелке. В (N+2)-ой строке указано количество селений K (0 ≤ K ≤ 100), а в последующих K строках заданы координаты селений. Все координаты - целые числа, не превосходящие по модулю 106. Размерами селений следует пренебречь
В выходной файл нужно вывести координаты любых двух различных точек, через которые следует провести границу. Координаты должны быть выведены с 6 знаками после десятичной точки.
Будут также оцениваться частичные решения для случая прямоугольного царства.
| input.txt | output.txt |
4 9 10 20 40 40 40 51 10 2 21 30 40 20 | 30.000000 35.000000 30.000000 15.000000 |
| Имя входного файла: | input.txt |
| Имя выходного файла: | output.txt |
| Ограничение по времени: | 5 секунд |
| Максимальная оценка: | 30 баллов |
Одна из проблем при игре на фортепьяно - выбор хорошей аппликатуры, то есть определение для каждого звука мелодии (клавиши инструмента) пальца руки, которым эту ноту лучше всего сыграть в данном месте мелодии.
Пронумеруем пальцы пианиста слева направо натуральными числами от 1 до P, клавиши инструмента также пронумеруем слева направо натуральными числами от 1 до K. Тогда запись звуков мелодии можно представить в виде последовательности N номеров клавиш, которые следует нажимать для ее исполнения, где N - длина мелодии.
Пусть для каждой пары пальцев с номерами i и j заданы целые числа aij и bij, такие, что если палец i нажимает клавишу X, то следующей клавишей пальцем j может быть нажата лишь клавиша из диапазона [X+aij, X+bij]. Этот набор чисел aij, bij, 1 ≤ i ≤ P , 1 ≤ j ≤ P, зависит от особенностей пианиста и его исполнительской техники. Заметим, что не каждая мелодия может быть сыграна конкретным пианистом при указанных выше ограничениях.
Назовем перекладыванием пальцев ситуацию, когда для двух последовательно исполняемых нот мелодии клавиша с большим номером нажимается пальцем с меньшим номером. Требуется написать программу, которая для заданной мелодии определяет аппликатуру с наименьшим количеством перекладываний пальцев.
В первой строке входного файла содержится число P - количество пальцев у пианиста (1 ≤ P ≤ 20). Во второй строке записано число K - количество клавиш у инструмента (1 ≤ K ≤ 10000). В третьей строке указаны целые числа a11 b11 a12 b12 ... a1P b1P a21 b21 a22 b22 ... a2P b2P ... aP1 bP1 aP2 bP2 ... aPP bPP, разделенные пробелами (-K ≤ aij ≤ bij ≤ K). В четвертой строке находится число N - длина мелодии (1 ≤ N ≤ 1000). Пятая строка содержит N чисел X1 X2 ... XN - последовательность разделенных пробелами номеров клавиш для исполнения мелодии.
В первой строке выходного файла должно содержаться либо число L - количество перекладываний пальцев в оптимальной аппликатуре, либо число -1 при невозможности сыграть мелодию. Вторая строка при наличии решения должна содержать N чисел Y1 ... YN - последовательность разделенных пробелами номеров пальцев при исполнении мелодии.
| input.txt | output.txt |
3 10 0 0 -2 -2 -5 1 2 3 8 10 0 1 2 10 -2 -2 -1 -1 9 4 5 7 7 7 6 8 7 5 | 3 2 3 1 1 3 3 1 3 2 |
| Имя входного файла: | input.txt |
| Имя выходного файла: | output.txt |
| Ограничение по времени: | 10 секунд |
| Максимальная оценка: | 40 баллов |
Простым высказыванием называется простое повествовательное предложение, относительно которого можно сказать, что оно истинно или ложно. Примерами таких высказываний являются предложения:
Одно из слов простого высказывания на русском языке назовем определяющим, если в результате добавления перед ним частицы НЕ значение простого высказывания изменяется на противоположное. В первом примере таким словом является слово "весной", а во втором - "меньше".
Сложным высказыванием назовем два и более простых высказывания, соединенные союзами И, ИЛИ, оборотами ЕСЛИ ..., ТО ... и ... ТОГДА И ТОЛЬКО ТОГДА, КОГДА ... . Назовем эти союзы и обороты вместе с частицей НЕ логическими операциями, обозначив их следующим образом:
| НЕ... | !... |
| ...И... | ...&... |
| ...ИЛИ... | ...|... |
| ...ЕСЛИ..., ТО... | ...=>... |
| ...ТОГДА И ТОЛЬКО ТОГДА, КОГДА... | ...<=>... |
Значение сложного высказывания можно определить, используя таблицы истинности логических операций. Приведем таблицы истинности перечисленных операций, обозначив ложное значение нулем, а истинное - единицей:
| A | !A |
| 0 | 1 |
| 1 | 0 |
| A | B | A&B | A|B | A=>B | A<=>B |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
В сложном высказывании операции имеют следующие приоритеты в порядке от высшего к низшему: !, &, |, =>, <=>. Например, в выражении A<=>!B=>C|D&E операции будут выполняться в таком порядке: (A<=>((!B)=>(C|(D&E)))). Здесь и далее в качестве имен высказываний будем использовать большие буквы латинского алфавита.
Рассмотрим следующую последовательность описаний.
В указанной последовательности описаний имя каждого следующего высказывания обозначается не встречавшейся ранее буквой. Высказывание, построенное последним, назовем результирующим высказыванием.
В первой строке входного файла содержится число N, задающее количество описаний в последовательности. В последующих N строках записаны описания по определенным выше правилам, каждое описание - в отдельной строке. Простые высказывания обозначаются буквами из диапазона от A до J и имеют длину не более 50 символов. Сложные высказывания обозначаются буквами из диапазона от K до T, пробелы в их определениях отсутствуют. В конце файла может содержаться одна или несколько пустых строк.
В выходном файле должны находиться 3 строки, каждая из которых является ответом на соответствующие пункты задания. Вторая строка должна содержать не более 50000 символов. В третьей строке слова, заменяющие логические операции, записываются заглавными русскими буквами и отделяются от простых высказываний пробелами. При отсутствии решения по какому-либо из пунктов задания соответствующая этому пункту строка должна быть пустой. Если в выходном файле вторая строка пустая, то ответ на пункт 3 оцениваться не будет.
Оба примера выходного файла являются допустимыми для приведенного входного файла.
| input.txt | output.txt |
6 A=(шел) дождь В=асфальт (мокрый) C=(хочется) гулять K=А&B L=!К М=L=>C | ((!(A&B))=>C) ((!A|!B)=>C) ЕСЛИ НЕ шел дождь ИЛИ асфальт НЕ мокрый, ТО хочется гулять |
((!(A&B))=>C) C|A&B&!C хочется гулять ИЛИ шел дождь И асфальт мокрый И НЕ хочется гулять |
| Имя входного файла: | input.txt |
| Имя выходного файла: | output.txt |
| Ограничение по времени: | 5 секунд |
| Максимальная оценка: | 30 баллов |
Известный ученый Яков Трахтенберг разработал систему быстрого счета для нахождения произведения двух натуральных чисел. Так, вычисление произведения 23 и 14 давало в качестве промежуточного результата последовательность чисел 12 11 2, называемую набором Трахтенберга. Далее по этому набору получался конечный результат, равный 322.
Приведем еще несколько примеров таких наборов:
| 241304 * 32 => 8 12 6 11 11 16 6 => 7721728 |
| 527 * 463 => 21 48 55 38 20 => 244001 |
| 3214 * 5643 => 12 19 34 43 29 28 15 => 18136602 |
| 1245 * 8 => 40 32 16 8 => 9960 |
Требуется определить, по какой схеме производилось умножение и составить программу, которая по заданному набору Трахтенберга восстанавливает все возможные пары сомножителей и определяет их произведения.
Во входном файле в одной строке записана последовательность чисел, разделенных пробелом, задающих некоторый набор Трахтенберга. Количество чисел в наборе не более 50.
Выведите в выходной файл искомые пары сомножителей и их произведения в формате:
Старшие цифры сомножителей и результата произведения не могут равняться нулю.
| input.txt | output.txt |
8 12 6 11 11 16 6 | 241304*32=7721728 |