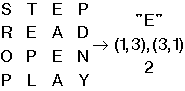 б)
б)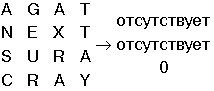
На вход "черного ящика" подается любая таблица, содержащая символы латинского алфавита. На выходе получается 3 строки результата. Например:
а) 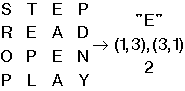 б)
б)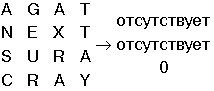
Опишите алгоритм, по которому мог бы работать этот "черный ящик".
Географическая карта местности задана квадратной сеткой определенного масштаба. В узлах сетки известна высота над уровнем моря. Между соседними узлами высота меняется плавно. Караван перемещается только по линиям сетки. (Перемещение по диагонали запрещается). Путь между двумя соседними точками с углом наклона больше 45 градусов считается непроходимым.
Провести караван из точки А(X1, Y1) в точку В(X2, Y2) по пути с наименьшим перепадом высоты или сообщить об отсутствии решения.
Примечание: Перепадом высот на маршруте называется разность высот между самой высокой и самой низкой точками маршрута.
В одной из клеток поля n × n (n > 1) Кощей Бессмертный спрятал Марью Царевну, создав еще неизвестное число m (1 < m < n × n) ее двойников в различных свободных клетках. И царевна, и ее двойники одинаково надежно укрыты и невидимы.
Отправившийся на поиски царевны Иванушка-дурачок попросил у благоволящей к нему щуки датчик биосигналов. Известно, что и Марья Царевна и ее двойники испускают незатухающие направленные биолучи, распространяющиеся параллельно сторонам и диагоналям поля.
Иванушка-дурачок также знает, что интенсивность биолуча Марьи Царевны в m раз выше интенсивности биолучей двойников. Иванушка может установить свой датчик в любую клетку поля и получить величину суммарной интенсивности биолучей, приходящих в клетку.
Помогите Иванушке определить местонахождение настоящей царевны.
Фирма "Школьник" предлагает разработать для электронных часов младших школьников режимы работы и трехкнопочную систему управления ими.
Опишите режимы работы часов, содержание отображаемой информации в каждом из режимов, функции кнопок.
Не забудьте, что это часы для младших школьников. Они должны быть просты в управлении. На них нецелесообразно иметь большое количество режимов работы.
Прямоугольная область задана своими координатами: (X1,Y1) - левая верхняя вершина и (X2,Y2) - правая нижняя вершина. По границе области ползет удав длины L со скоростью V. Внутри области движется точка со скоростью V1. Точка начинает движение вниз от границы области на заданном расстоянии S от ее верхнего левого угла и под углом A к нижней линии области. Точка движется, отражаясь от стенок до тех пор, пока не столкнется с удавом. Объекты начинают движение одновременно.
Составить программу, вычисляющую количество отражений точки от границ области и время до столкновения с удавом. Если при стократном отражении точка не столкнулась с удавом, программа прекращает работу, сообщив об этом событии.
Расположенную вертикально прямоугольную бумажную ленточку с закрепленным нижним концом стали складывать следующим образом: